tna — R Package Documentation • tna

tna provides tools for performing Transition Network Analysis (TNA) to study relational dynamics. Build Markov models from sequence data, compute centrality measures, detect communities and cliques, and validate findings with bootstrapping and permutation tests.

Install:

install.packages("tna")
# or dev version:
devtools::install_github("sonsoleslp/tna")

Requires R >= 4.1.0. All analysis objects have print(), summary(), and plot() methods.

Building Models

`build_model()`

Construct a transition network analysis model from sequence data. Requires specifying type. For convenience, use the shortcut functions: tna() = relative, ftna() = frequency, ctna() = co-occurrence, atna() = attention.

build_model(x, type = "relative", scaling = character(0L), cols = everything(),
            params = list(), inits, begin_state, end_state)

Parameter	Description	Default
`x`	`data.frame` (wide), `stslist`, `matrix`, or `tna_data`	—
`type`	`"relative"`, `"frequency"`, `"co-occurrence"`, `"n-gram"`, `"gap"`, `"window"`, `"reverse"`, `"attention"`	`"relative"`
`scaling`	`"minmax"`, `"max"`, `"rank"`, or empty vector	`character(0)`
`params`	List: `n_gram`, `max_gap`, `window_size`, `weighted`, `direction`, `decay`, `lambda`, `time`, `duration`	`list()`

Returns: A tna object with $weights, $inits, $labels, $data.

# Using build_model with explicit type
model <- build_model(group_regulation, type = "relative")

# Shortcut functions (preferred)
model <- tna(group_regulation)       # type = "relative"
model_f <- ftna(group_regulation)    # type = "frequency"
model_c <- ctna(group_regulation)    # type = "co-occurrence"
model_a <- atna(group_regulation)    # type = "attention"

print(model)

#> State Labels : 
#> 
#>    adapt, cohesion, consensus, coregulate, discuss, emotion, monitor, plan, synthesis 
#> 
#> Transition Probability Matrix :
#> 
#>                   adapt   cohesion  consensus coregulate    discuss    emotion
#> adapt      0.0000000000 0.27308448 0.47740668 0.02161100 0.05893910 0.11984283
#> cohesion   0.0029498525 0.02713864 0.49793510 0.11917404 0.05958702 0.11563422
#> consensus  0.0047400853 0.01485227 0.08200348 0.18770738 0.18802338 0.07268131
#> coregulate 0.0162436548 0.03604061 0.13451777 0.02335025 0.27360406 0.17208122
#> discuss    0.0713743356 0.04758289 0.32118451 0.08428246 0.19488737 0.10579600
#> emotion    0.0024673951 0.32534367 0.32040888 0.03419105 0.10186817 0.07684173
#> monitor    0.0111653873 0.05582694 0.15910677 0.05792045 0.37543615 0.09071877
#> plan       0.0009745006 0.02517460 0.29040117 0.01721618 0.06789021 0.14682475
#> synthesis  0.2346625767 0.03374233 0.46625767 0.04447853 0.06288344 0.07055215
#>               monitor       plan   synthesis
#> adapt      0.03339882 0.01571709 0.000000000
#> cohesion   0.03303835 0.14100295 0.003539823
#> consensus  0.04661084 0.39579712 0.007584137
#> coregulate 0.08629442 0.23908629 0.018781726
#> discuss    0.02227284 0.01164262 0.140976968
#> emotion    0.03630596 0.09975326 0.002819880
#> monitor    0.01814375 0.21563154 0.016050244
#> plan       0.07552379 0.37420822 0.001786584
#> synthesis  0.01226994 0.07515337 0.000000000
#> 
#> Initial Probabilities : 
#> 
#>      adapt   cohesion  consensus coregulate    discuss    emotion    monitor 
#>     0.0115     0.0605     0.2140     0.0190     0.1755     0.1515     0.1440 
#>       plan  synthesis 
#>     0.2045     0.0195

summary(model)

#> # A tibble: 13 × 2
#>    metric                         value
#>  * <chr>                          <dbl>
#>  1 Node Count                  9   e+ 0
#>  2 Edge Count                  7.8 e+ 1
#>  3 Network Density             1   e+ 0
#>  4 Mean Distance               4.72e- 2
#>  5 Mean Out-Strength           1   e+ 0
#>  6 SD Out-Strength             8.07e- 1
#>  7 Mean In-Strength            1   e+ 0
#>  8 SD In-Strength              6.80e-17
#>  9 Mean Out-Degree             8.67e+ 0
#> 10 SD Out-Degree               7.07e- 1
#> 11 Centralization (Out-Degree) 1.56e- 2
#> 12 Centralization (In-Degree)  1.56e- 2
#> 13 Reciprocity                 9.86e- 1

Model types

Type	Description
`"relative"`	Transition probabilities (rows sum to 1). Default
`"frequency"`	Raw transition counts
`"co-occurrence"`	Co-occurrence within sequences
`"n-gram"`	Higher-order transitions
`"gap"`	Non-adjacent transitions, weighted by gap
`"window"`	Transitions within sliding window
`"reverse"`	Reverse order (reply networks)
`"attention"`	Exponential decay-weighted downstream pairs

`group_model()` / `group_tna()`

Build a TNA model for each group. Accepts manual group assignments, mhmm objects, or tna_clustering results. Most tna functions accept group_tna directly — no need to specify groups again.

group_model(x, group, type = "relative", scaling = character(0L),
            groupwise = FALSE, cols = everything(), params = list(), na.rm = TRUE, ...)

# From mixture Markov model
model <- group_model(engagement_mmm)
print(model)

#> Cluster 1 :
#> State Labels : 
#> 
#>    Active, Average, Disengaged 
#> 
#> Transition Probability Matrix :
#> 
#>                Active    Average Disengaged
#> Active     0.85985688 0.08919748 0.05094565
#> Average    0.31210322 0.54208478 0.14581200
#> Disengaged 0.04791061 0.16179397 0.79029542
#> 
#> Initial Probabilities : 
#> 
#>     Active    Average Disengaged 
#>  0.3397762  0.3234995  0.3367243 
#> 
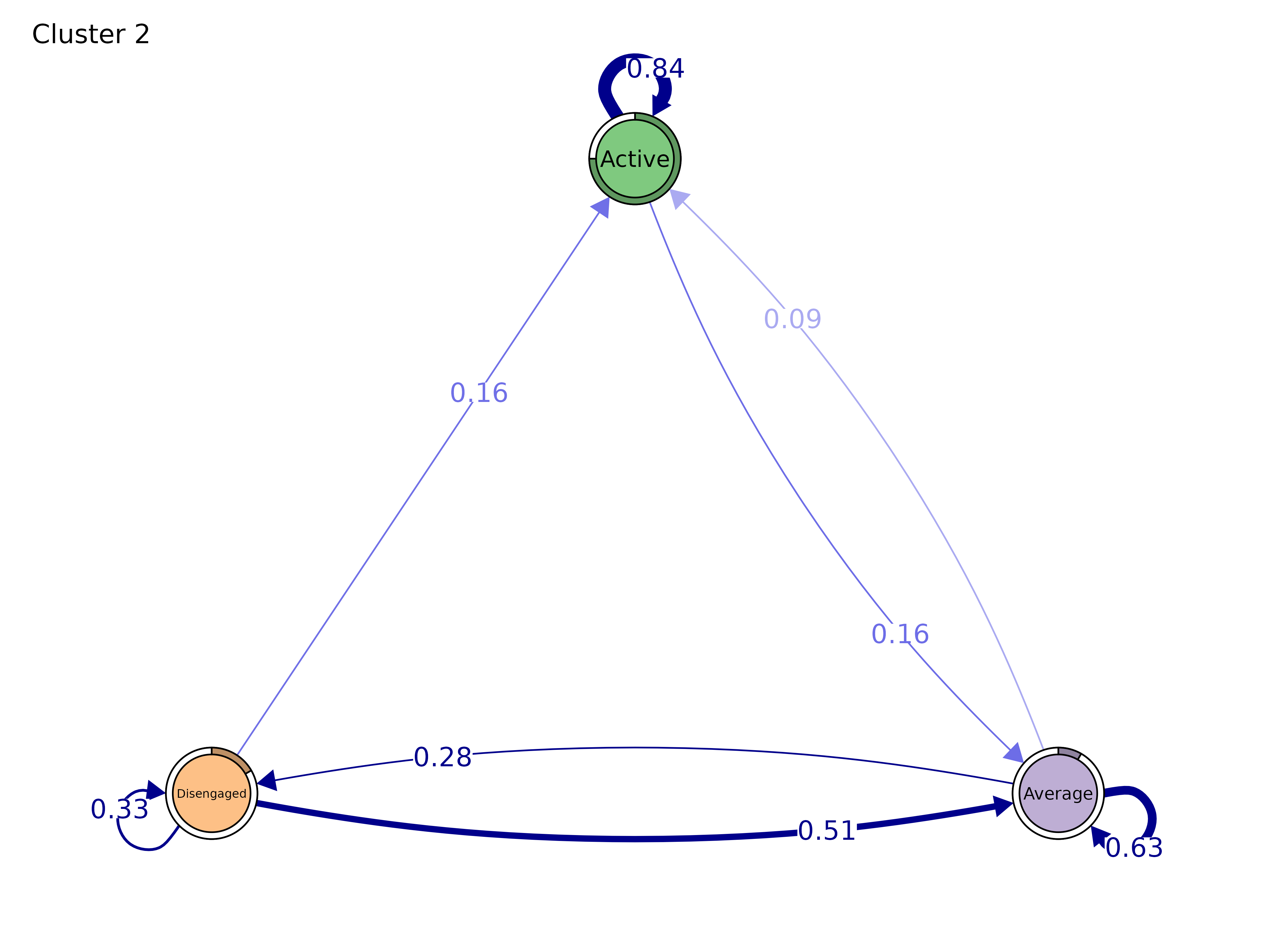
#> Cluster 2 :
#> State Labels : 
#> 
#>    Active, Average, Disengaged 
#> 
#> Transition Probability Matrix :
#> 
#>                Active   Average Disengaged
#> Active     0.84090909 0.1590909  0.0000000
#> Average    0.09259259 0.6296296  0.2777778
#> Disengaged 0.15555556 0.5111111  0.3333333
#> 
#> Initial Probabilities : 
#> 
#>     Active    Average Disengaged 
#> 0.75000000 0.08333333 0.16666667 
#> 
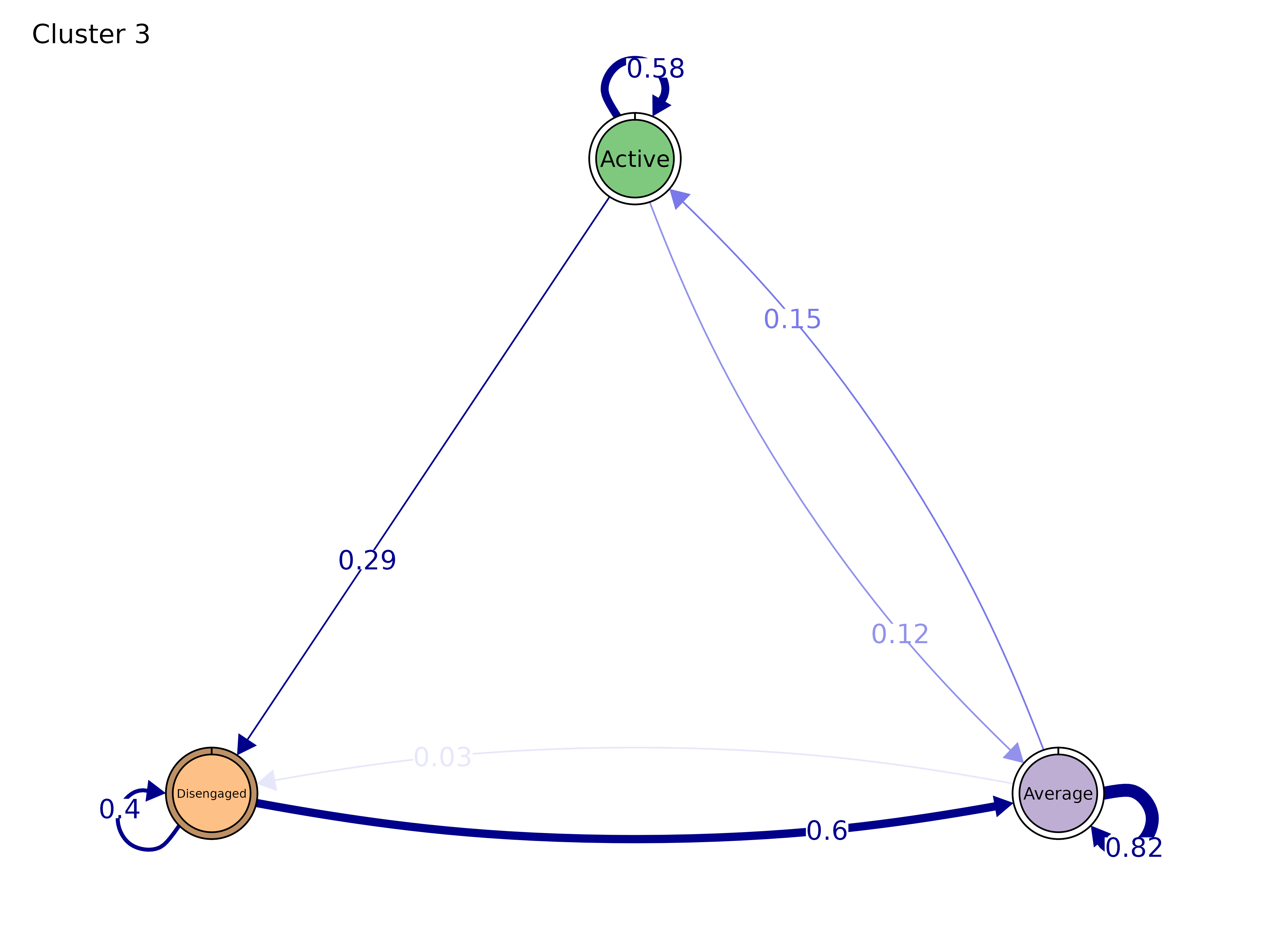
#> Cluster 3 :
#> State Labels : 
#> 
#>    Active, Average, Disengaged 
#> 
#> Transition Probability Matrix :
#> 
#>               Active   Average Disengaged
#> Active     0.5833333 0.1250000 0.29166667
#> Average    0.1527778 0.8194444 0.02777778
#> Disengaged 0.0000000 0.6000000 0.40000000
#> 
#> Initial Probabilities : 
#> 
#>     Active    Average Disengaged 
#>          0          0          1

summary(model)

#> # A tibble: 13 × 4
#>    metric                      `Cluster 1` `Cluster 2` `Cluster 3`
#>  * <chr>                             <dbl>       <dbl>       <dbl>
#>  1 Node Count                        3           3           3    
#>  2 Edge Count                        9           8           8    
#>  3 Network Density                   1           1           1    
#>  4 Mean Distance                     0.111       0.239       0.302
#>  5 Mean Out-Strength                 1           1           1    
#>  6 SD Out-Strength                   0.214       0.353       0.472
#>  7 Mean In-Strength                  1           1           1    
#>  8 SD In-Strength                    0           0           0    
#>  9 Mean Out-Degree                   3           2.67        2.67 
#> 10 SD Out-Degree                     0           0.577       0.577
#> 11 Centralization (Out-Degree)       0           0.25        0.25 
#> 12 Centralization (In-Degree)        0           0.25        0.25 
#> 13 Reciprocity                       1           0.8         0.8

# Manual groups
group <- c(rep("High", 1000), rep("Low", 1000))
model <- group_model(group_regulation, group = group)

`sna()`

Build a social network analysis model from edge-list data (from, to, weight).

set.seed(42)
d <- data.frame(
  from = sample(LETTERS[1:4], 100, replace = TRUE),
  to = sample(LETTERS[1:4], 100, replace = TRUE),
  weight = rexp(100)
)
model_sna <- sna(d)

Plotting

All TNA analysis objects have plot() methods returning qgraph or ggplot2 objects.

`plot()`

Plot a TNA model as a transition network.

plot(x, labels, colors, pie, cut, show_pruned = TRUE, pruned_edge_color = "pink",
     edge.color = NA, edge.labels = TRUE, edge.label.position = 0.65,
     layout = "circle", layout_args = list(), scale_nodes, scaling_factor = 0.5,
     mar = rep(5, 4), theme = "colorblind", ...)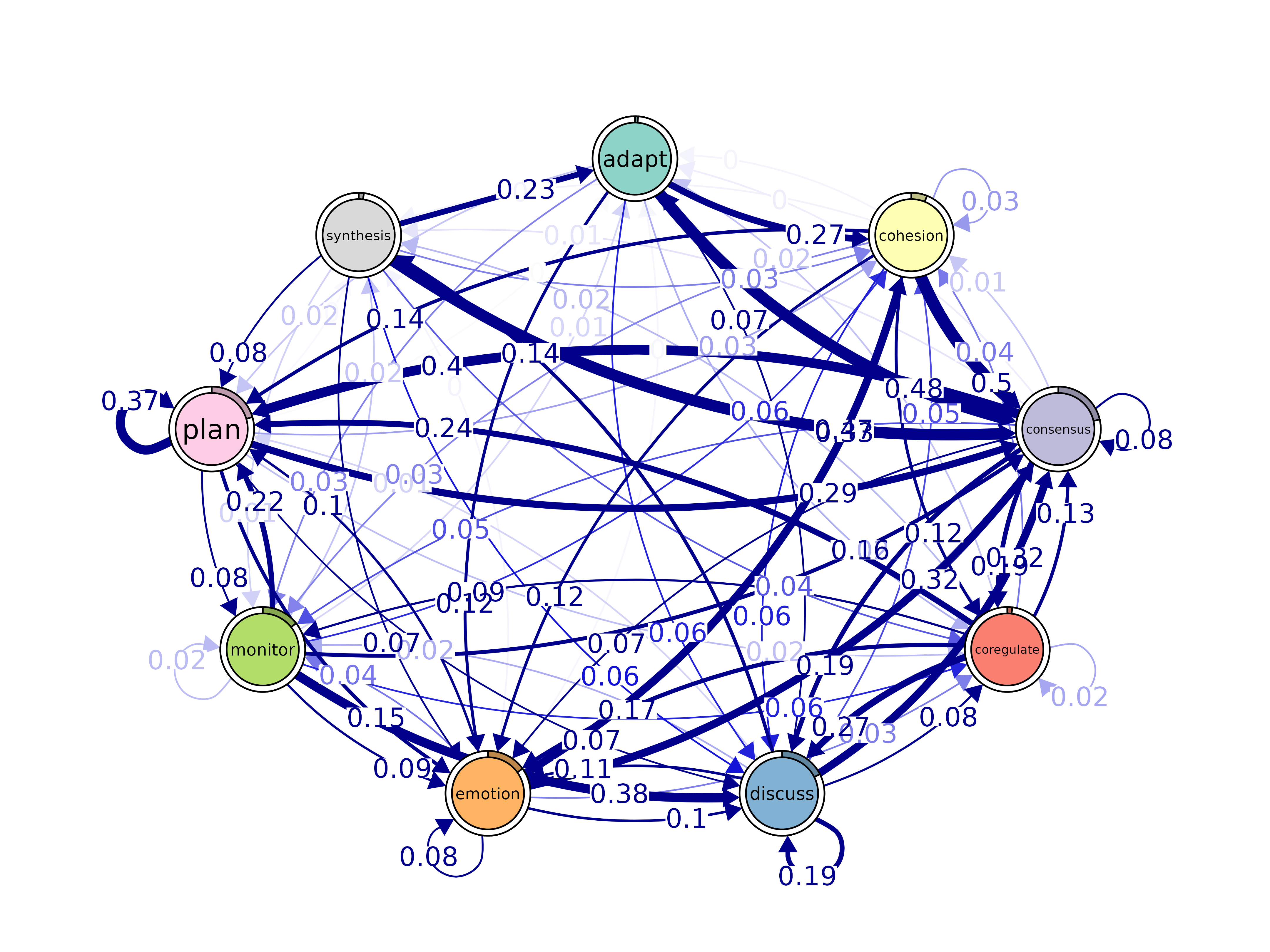

model <- tna(group_regulation)
plot(model)

plot(model, layout = "spring", scale_nodes = "OutStrength")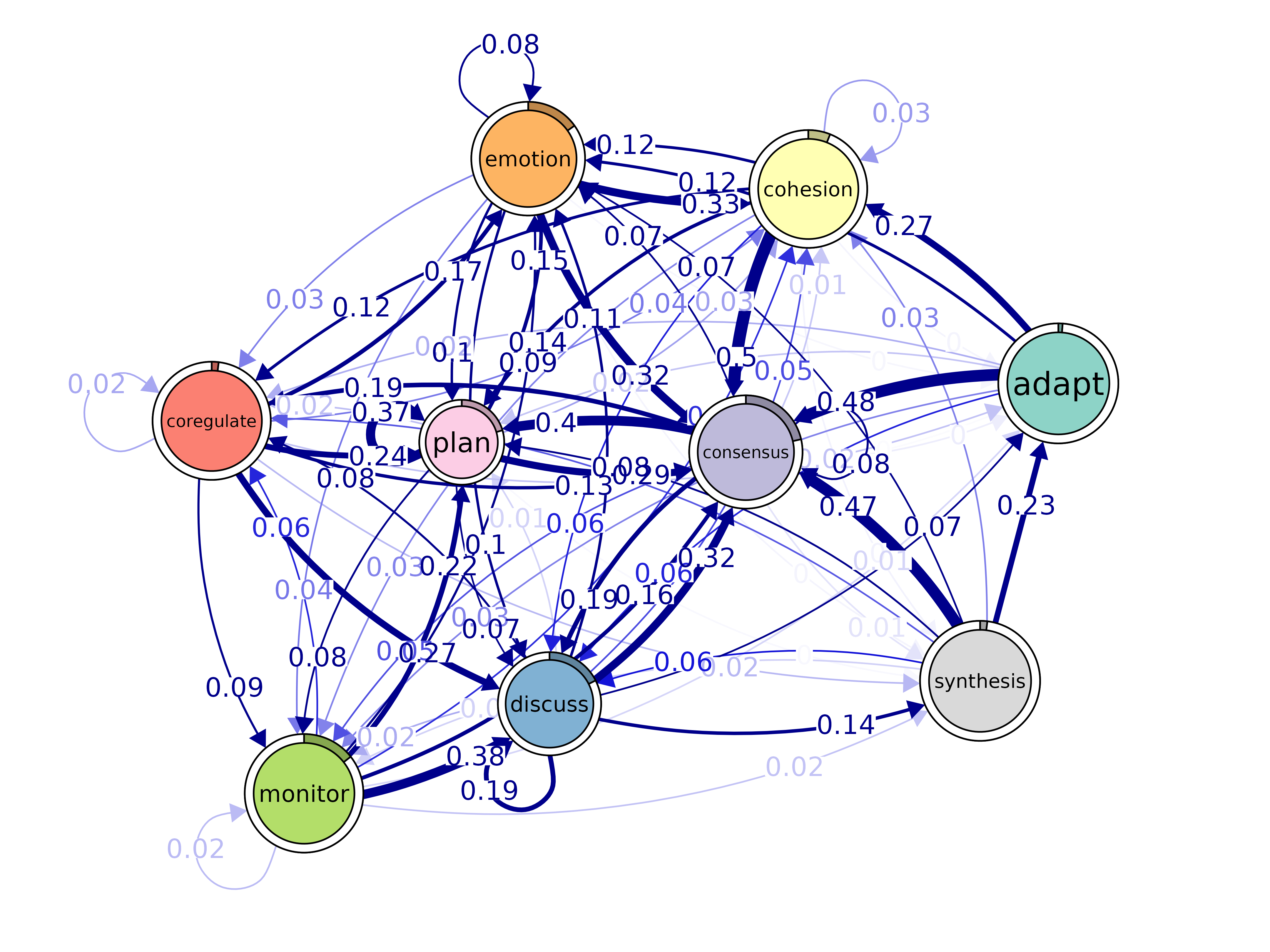

# Group model — side-by-side panels
gmodel <- group_model(engagement_mmm)
plot(gmodel)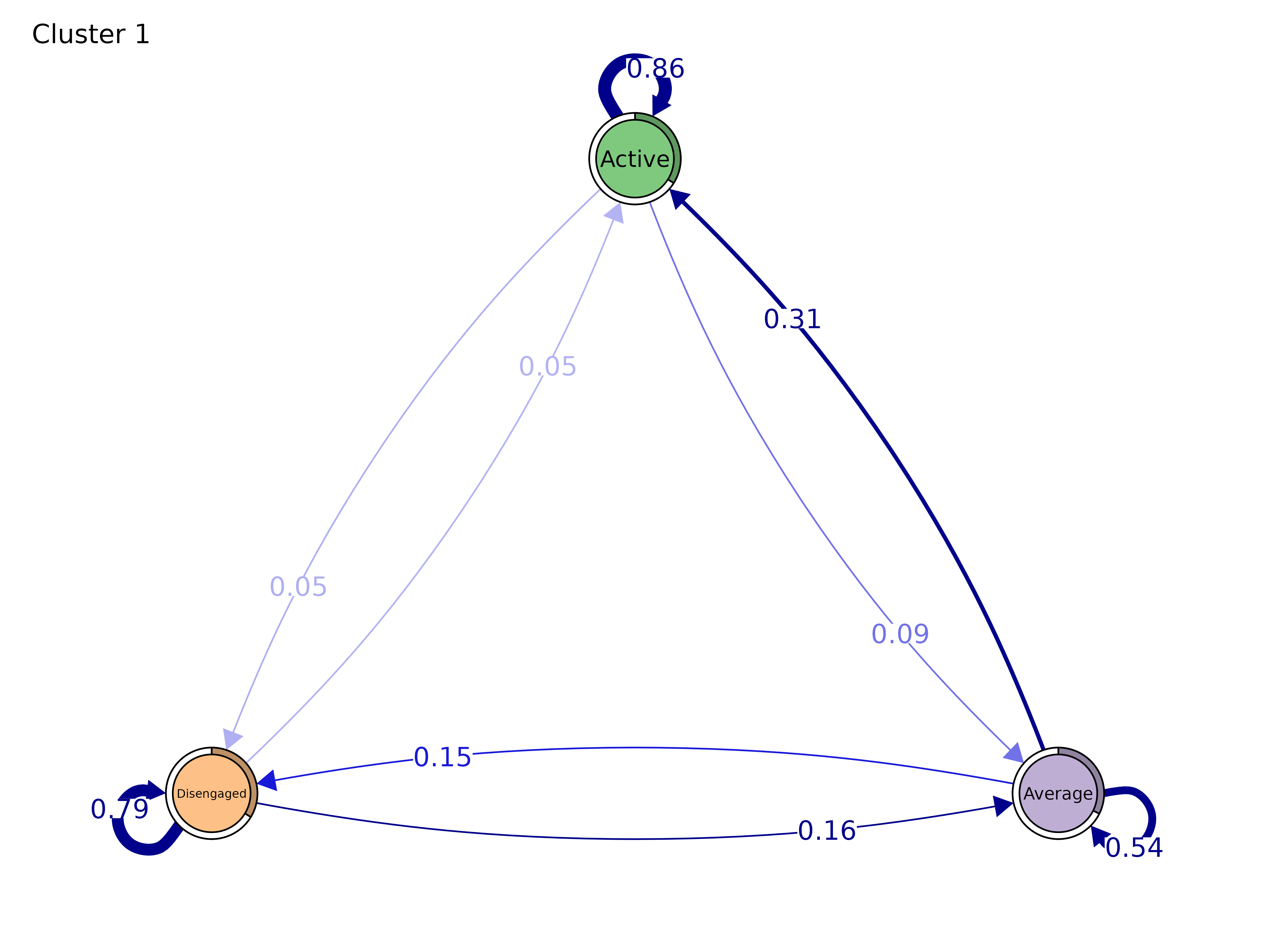

`plot_frequencies()`

Bar plot of state frequency distribution.

model <- tna(group_regulation)
plot_frequencies(model)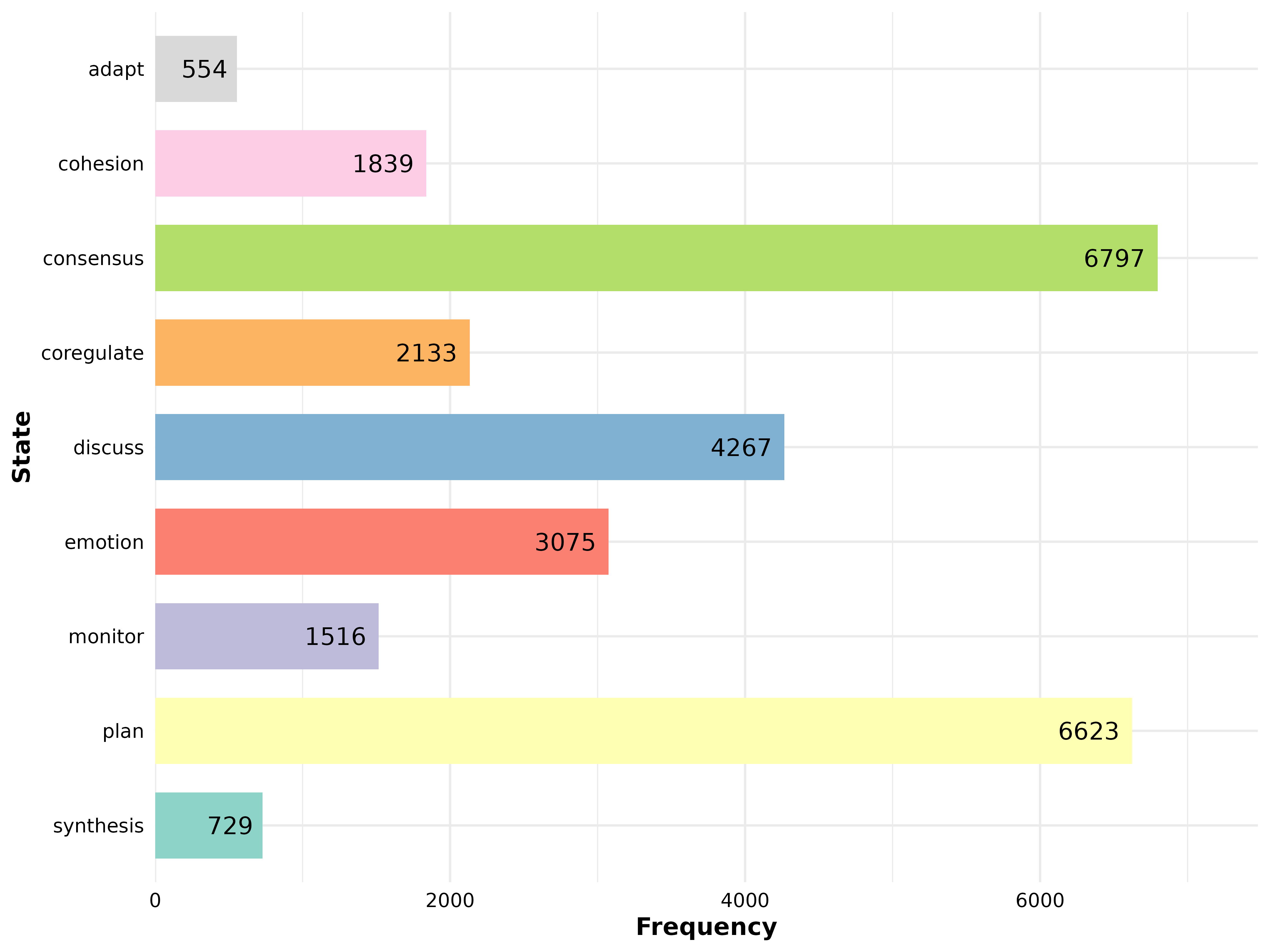

# Group comparison
gmodel <- group_model(engagement_mmm)
plot_frequencies(gmodel)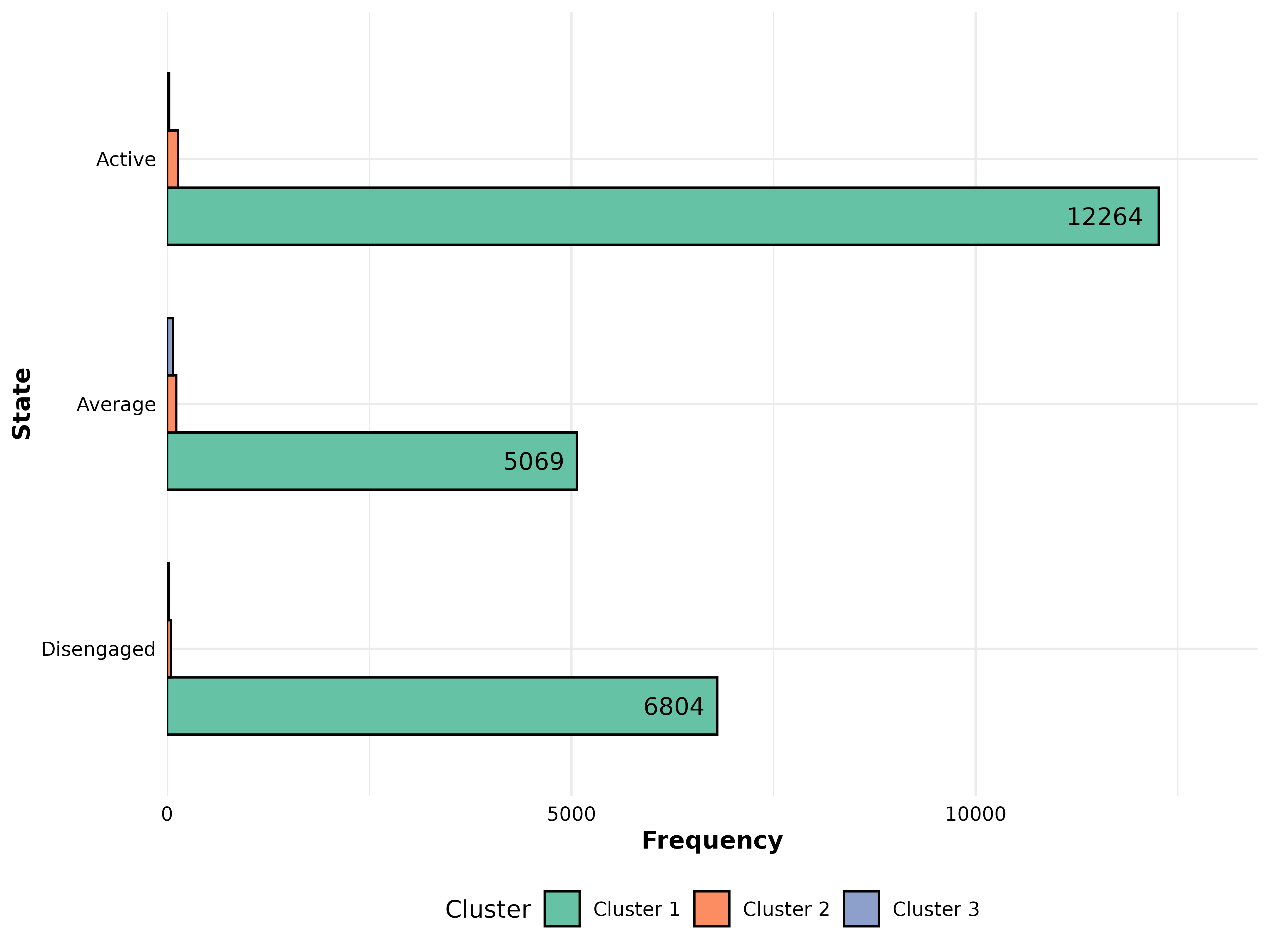

`plot_mosaic()`

Mosaic plot with chi-square test results. Requires frequency model (ftna()).

model_f <- ftna(group_regulation)
plot_mosaic(model_f)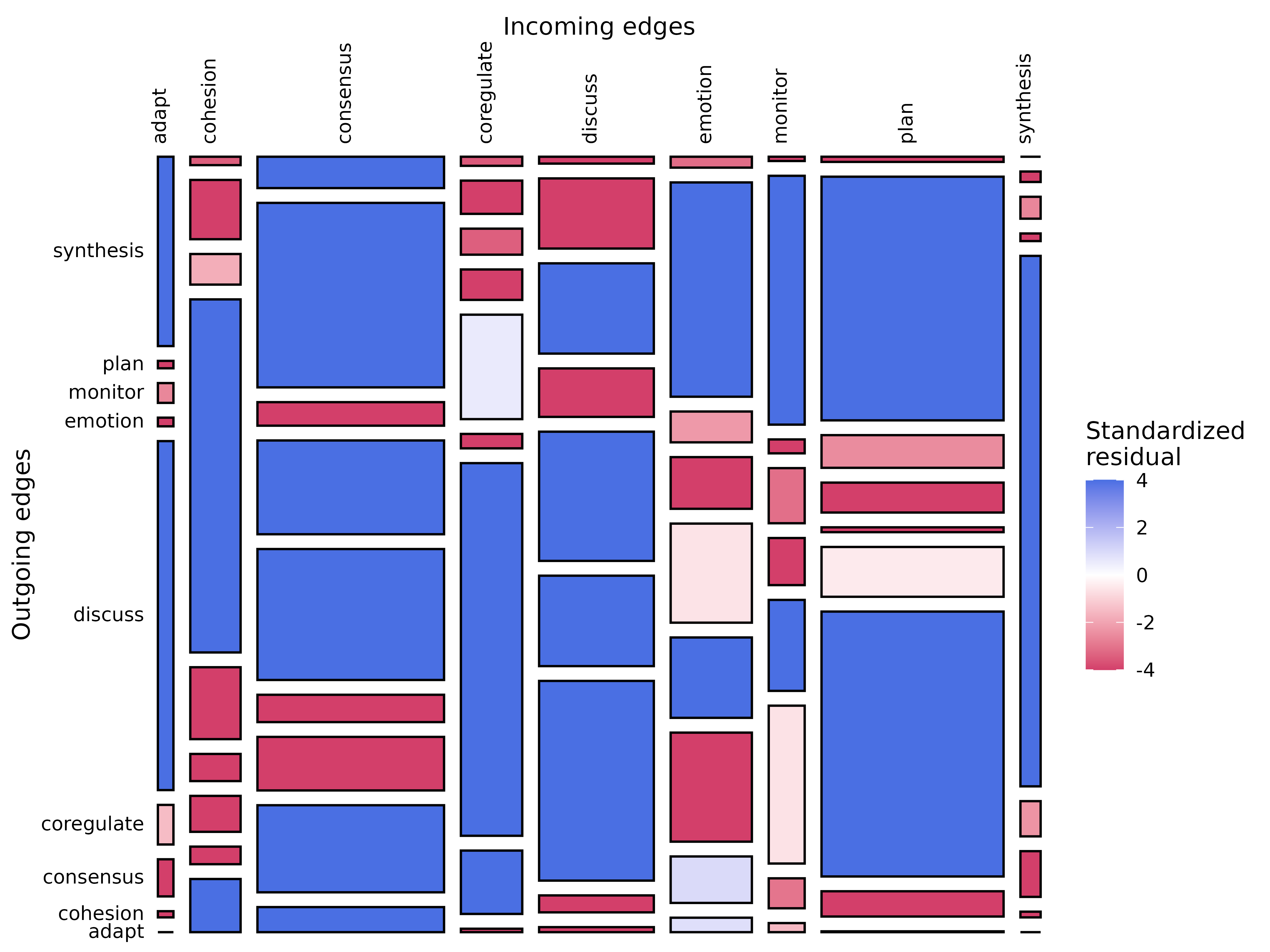

`plot_sequences()`

Sequence index plots or state distribution plots.

plot_sequences(x, cols = everything(), group, type = "index", scale = "proportion",
               geom = "bar", include_na = FALSE, colors, na_color = "white",
               sort_by, show_n = TRUE, border, title, legend_title, xlab, ylab,
               tick = 5, ncol = 2L, ...)

plot_sequences(group_regulation)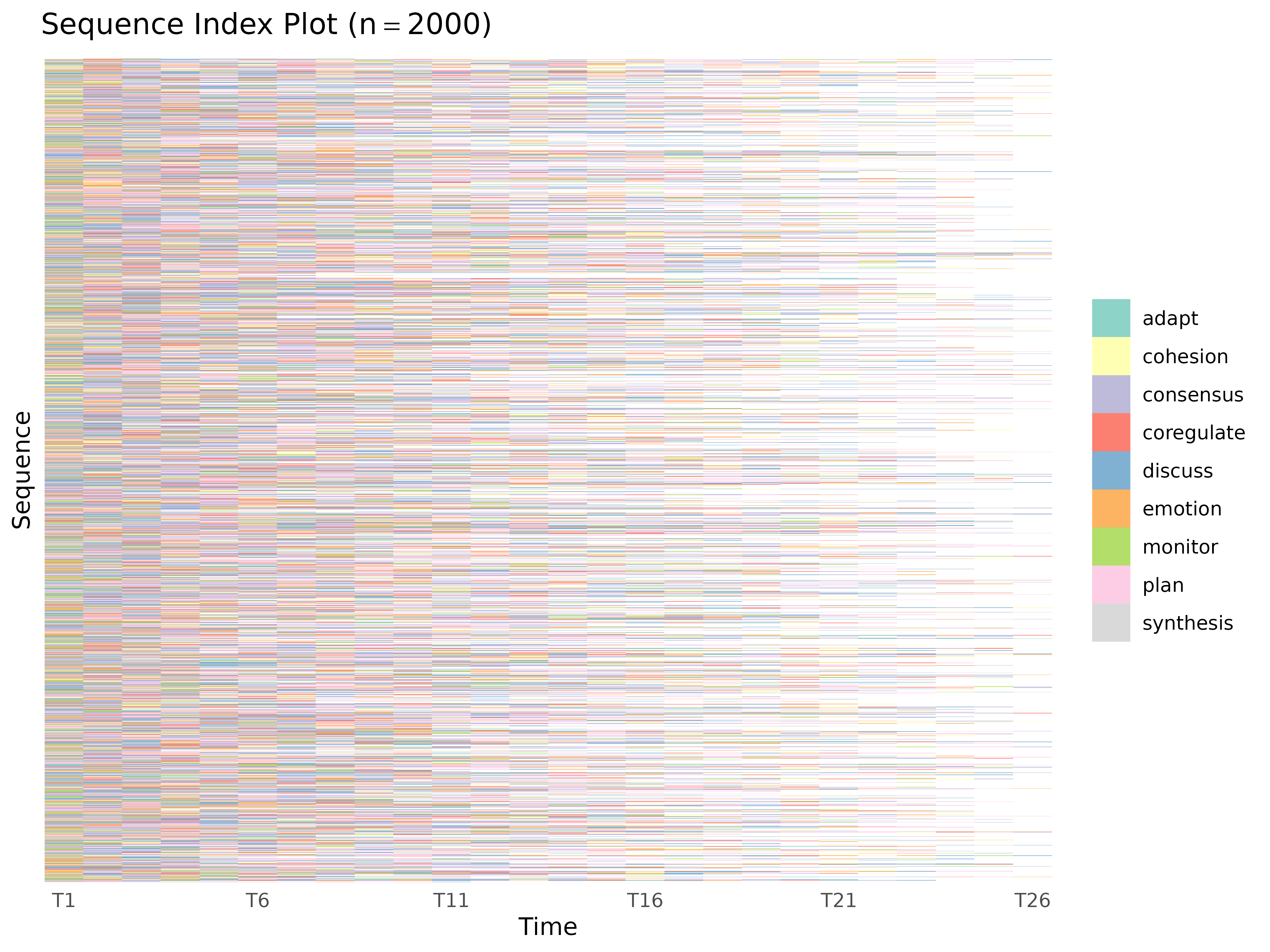

plot_sequences(group_regulation, type = "distribution")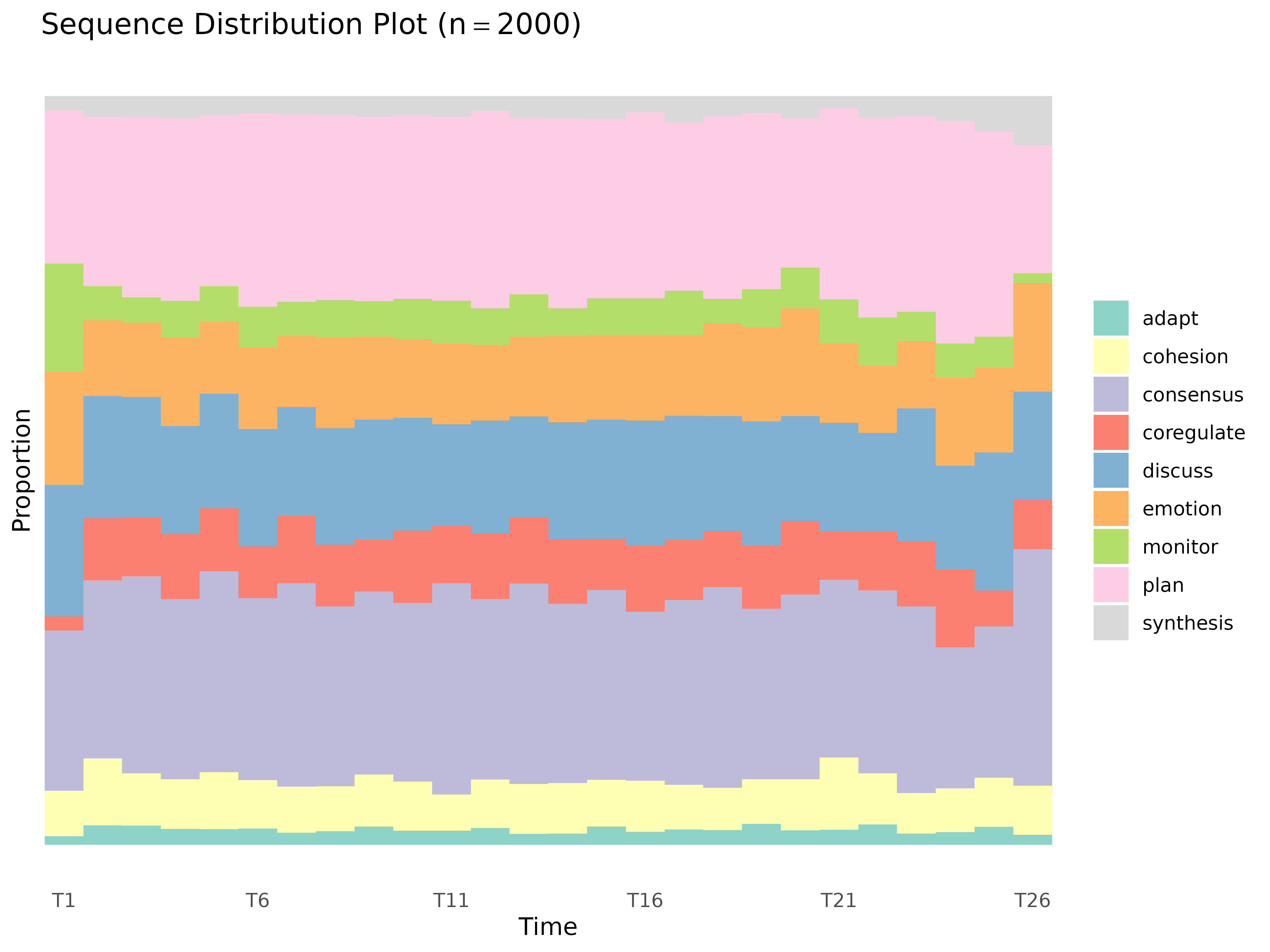

# Group comparison — pass group_tna directly
gmodel <- group_model(engagement_mmm)
plot_sequences(gmodel)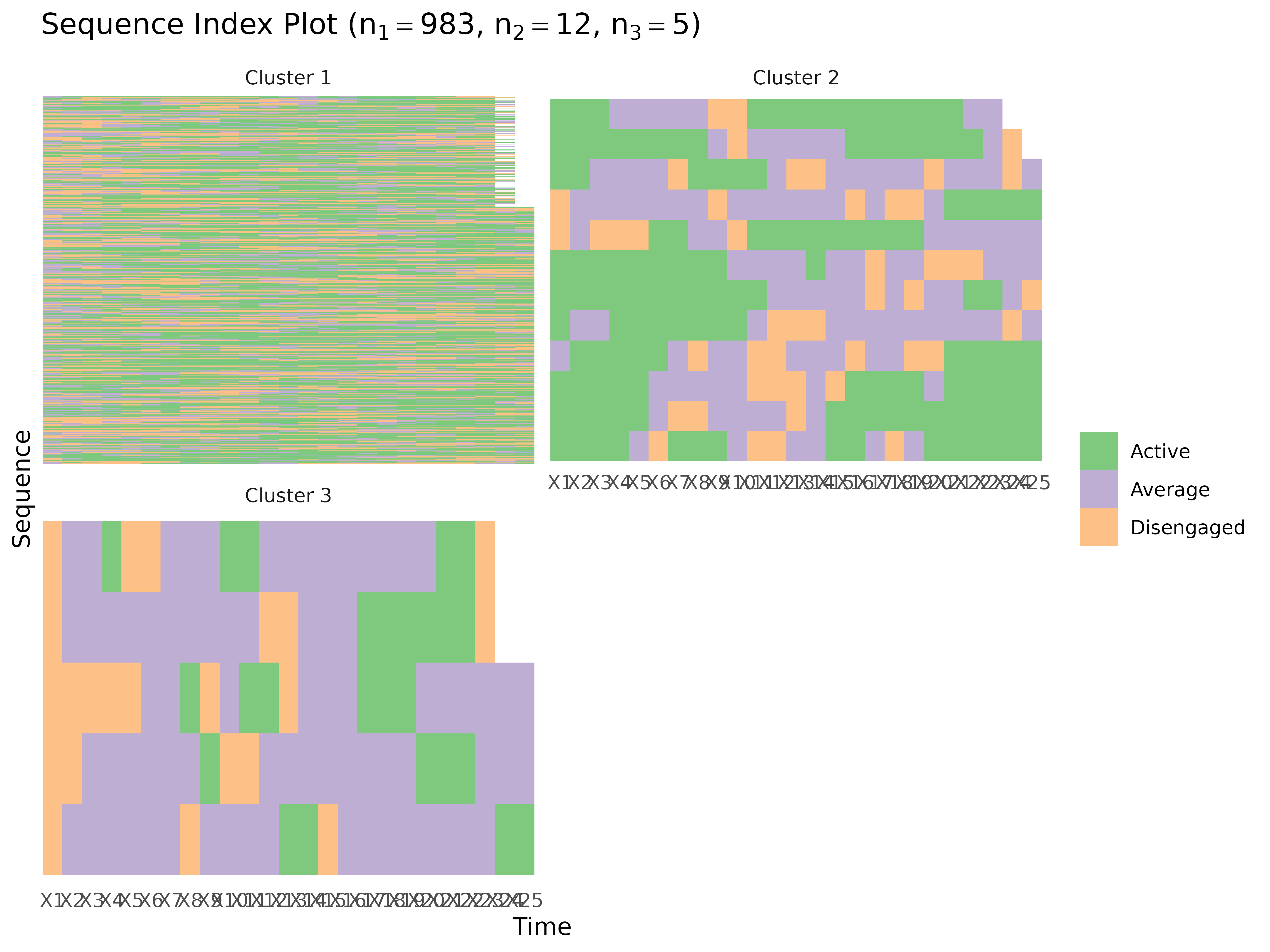

`plot_compare()`

Difference network between two models. Green = x greater, red = y greater.

model_a <- tna(group_regulation[1:1000, ])
model_b <- tna(group_regulation[1001:2000, ])
plot_compare(model_a, model_b)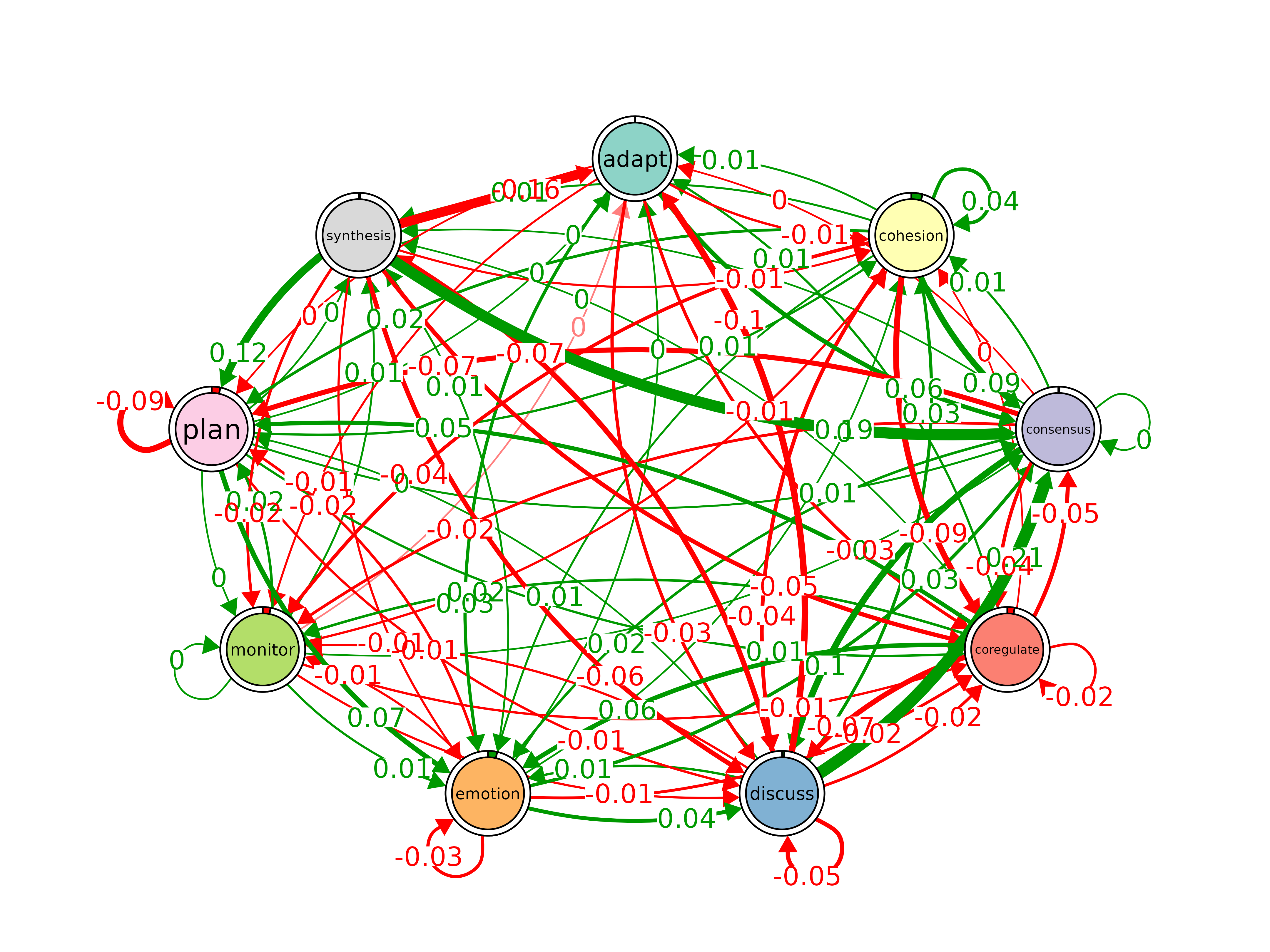

`plot_associations()`

Association network. Requires frequency model (ftna()).

model_f <- ftna(group_regulation)
plot_associations(model_f)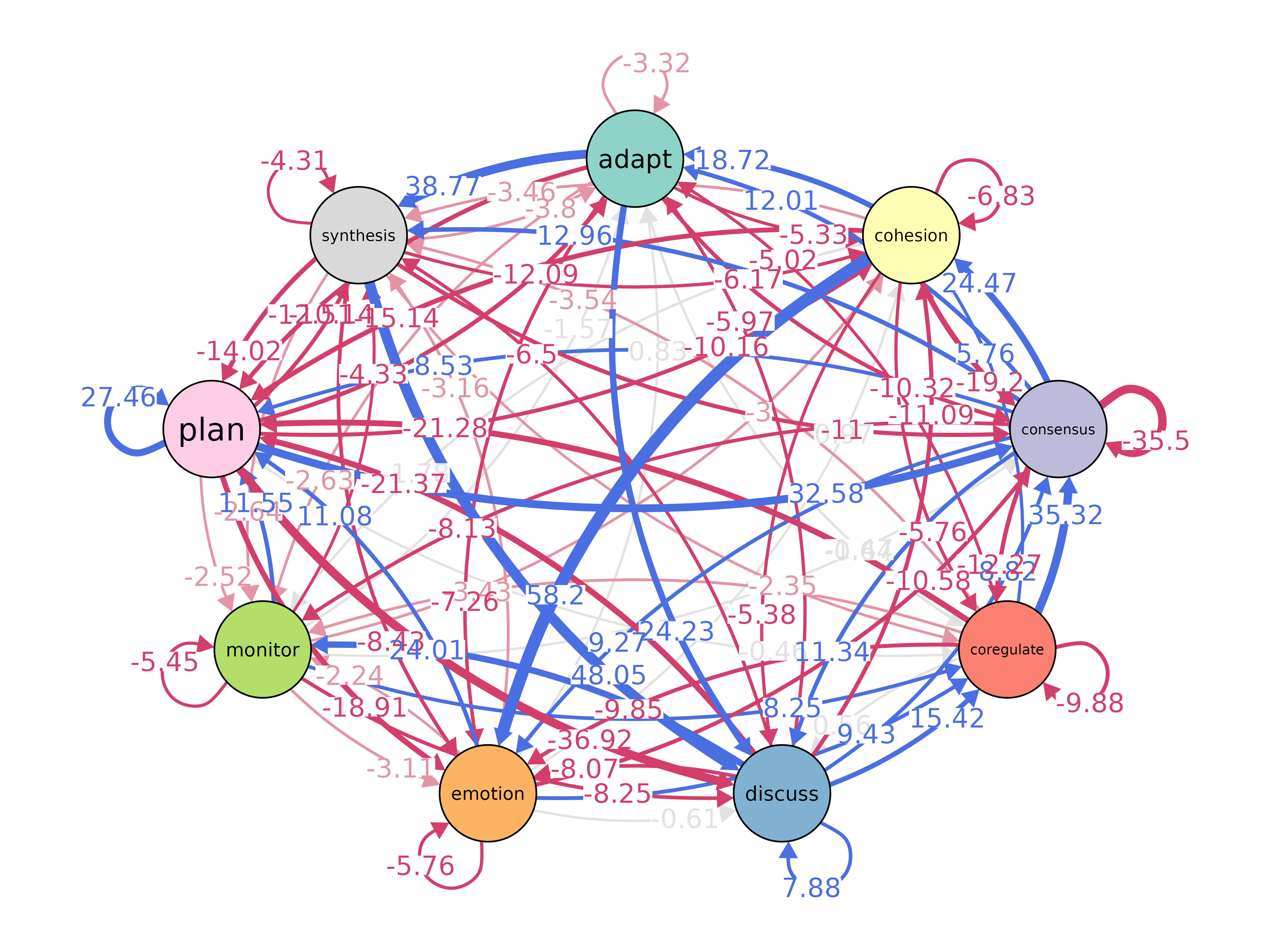

`hist()`

model <- tna(group_regulation)
hist(model)

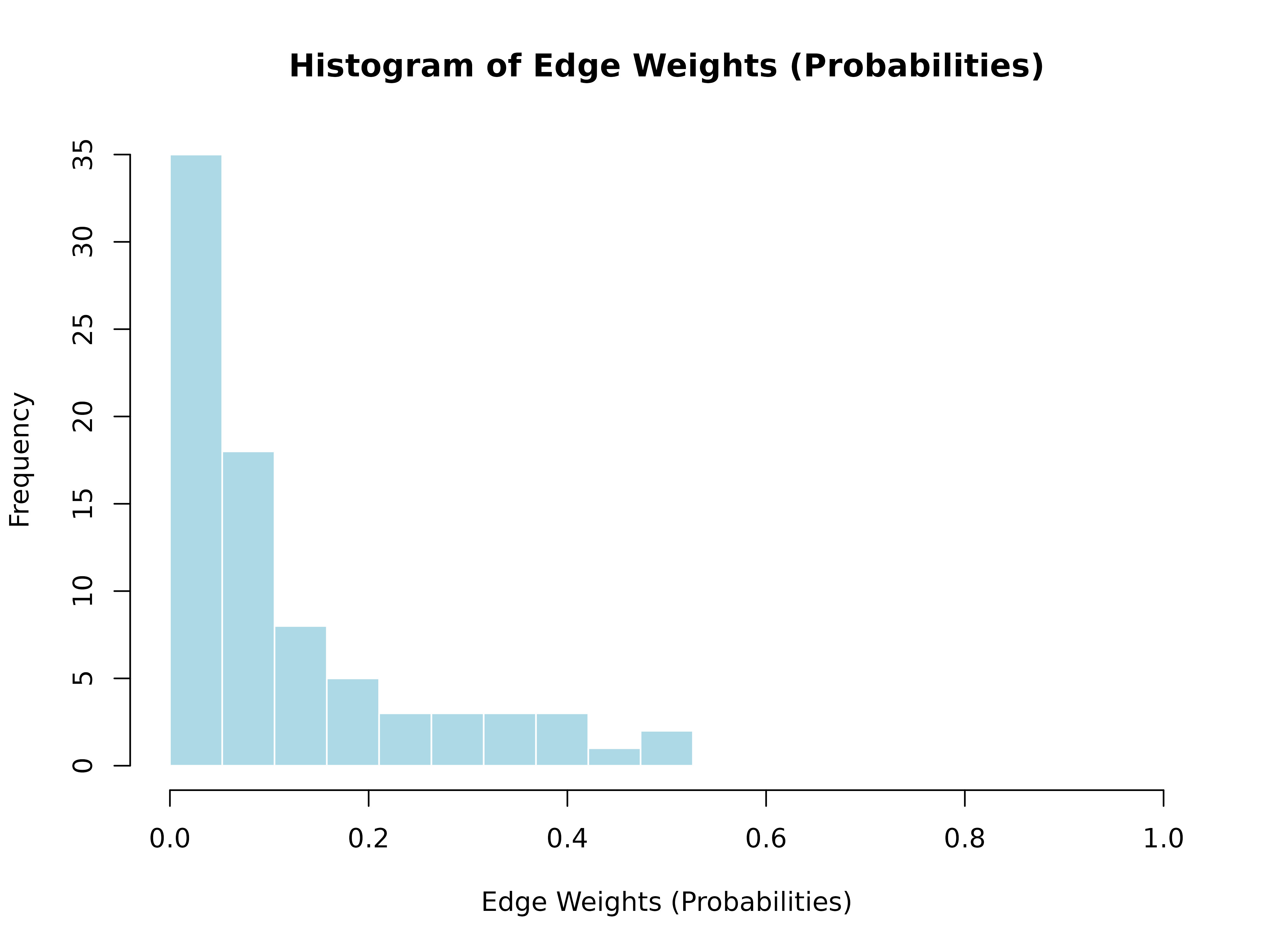
Additional plot methods

Object	plot() produces
`tna_centralities`	Lollipop charts by measure
`tna_communities`	Network colored by community
`tna_cliques`	Individual clique subnetworks
`tna_bootstrap`	Significant edges only
`tna_permutation`	Significant edge differences
`tna_stability`	Stability curves with CS-coefficients
`tna_comparison`	Heatmap or difference viz
`tna_sequence_comparison`	Pattern comparison chart
`group_tna`	Side-by-side network plots

Data Preparation

`prepare_data()`

Convert long-format event logs into wide-format sequences.

prepare_data(data, actor, time, action, order, time_threshold = 900,
             custom_format = NULL, is_unix_time = FALSE,
             unix_time_unit = "seconds", unused_fn = dplyr::first)

results <- prepare_data(
  group_regulation_long,
  actor = "Actor", time = "Time", action = "Action"
)
print(results$statistics)

#> $total_sessions
#> [1] 2000
#> 
#> $total_actions
#> [1] 27533
#> 
#> $max_sequence_length
#> [1] 26
#> 
#> $unique_users
#> [1] 2000
#> 
#> $sessions_per_user
#> # A tibble: 2,000 × 2
#>    Actor n_sessions
#>    <int>      <int>
#>  1     1          1
#>  2     2          1
#>  3     3          1
#>  4     4          1
#>  5     5          1
#>  6     6          1
#>  7     7          1
#>  8     8          1
#>  9     9          1
#> 10    10          1
#> # ℹ 1,990 more rows
#> 
#> $actions_per_session
#> # A tibble: 2,000 × 2
#>    .session_id   n_actions
#>    <chr>             <int>
#>  1 1010 session1        26
#>  2 1015 session1        26
#>  3 1030 session1        26
#>  4 1092 session1        26
#>  5 1106 session1        26
#>  6 1107 session1        26
#>  7 1153 session1        26
#>  8 1184 session1        26
#>  9 1209 session1        26
#> 10 1267 session1        26
#> # ℹ 1,990 more rows
#> 
#> $time_range
#> [1] "2025-01-01 08:01:16 UTC" "2025-01-01 13:03:20 UTC"

`import_data()`

Transform wide-format feature data into long-format sequence data.

import_data(data, cols, id_cols, window_size = 1, replace_zeros = TRUE)

`import_onehot()`

Import one-hot encoded data as co-occurrence network.

import_onehot(data, cols, window = 1L)

`simulate()`

Simulate sequence data from a TNA model (requires type = "relative").

model <- tna(group_regulation)
sim <- simulate(model, nsim = 5, seed = 123, max_len = 10)
print(sim)

#>         T1         T2        T3      T4        T5       T6         T7
#> 1     plan    emotion consensus monitor consensus  discuss  synthesis
#> 2  monitor    emotion      plan    plan   emotion     plan  consensus
#> 3     plan       plan      plan discuss   discuss cohesion coregulate
#> 4  monitor coregulate      plan    plan      plan     plan    monitor
#> 5 cohesion  consensus consensus    plan      plan  monitor    emotion
#>           T8         T9       T10
#> 1      adapt       plan      plan
#> 2    discuss   cohesion consensus
#> 3       plan  consensus      plan
#> 4 coregulate  consensus      plan
#> 5  consensus coregulate   monitor

Centrality Measures

`centralities()`

Calculate centrality measures. Works on tna, group_tna, and matrix.

centralities(x, loops = FALSE, normalize = FALSE, measures)

Measure	Description
`OutStrength`	Total weight of outgoing edges
`InStrength`	Total weight of incoming edges
`ClosenessIn` / `ClosenessOut` / `Closeness`	Closeness centrality variants
`Betweenness`	Geodesic betweenness
`BetweennessRSP`	Randomized shortest paths betweenness
`Diffusion`	Diffusion centrality
`Clustering`	Signed clustering coefficient

model <- tna(group_regulation)
cm <- centralities(model)
print(cm)

#> # A tibble: 9 × 10
#>   state    OutStrength InStrength ClosenessIn ClosenessOut Closeness Betweenness
#> * <fct>          <dbl>      <dbl>       <dbl>        <dbl>     <dbl>       <dbl>
#> 1 adapt          1          0.345     0.00834       0.0152    0.0248           1
#> 2 cohesion       0.973      0.812     0.0138        0.0124    0.0265           0
#> 3 consens…       0.918      2.67      0.0351        0.0125    0.0383          30
#> 4 coregul…       0.977      0.567     0.0155        0.0150    0.0210           0
#> 5 discuss        0.805      1.19      0.0196        0.0131    0.0271          16
#> 6 emotion        0.923      0.894     0.0141        0.0121    0.0231           5
#> 7 monitor        0.982      0.346     0.00758       0.0137    0.0193           0
#> 8 plan           0.626      1.19      0.0274        0.0115    0.0274           9
#> 9 synthes…       1          0.192     0.00997       0.0158    0.0243           7
#> # ℹ 3 more variables: BetweennessRSP <dbl>, Diffusion <dbl>, Clustering <dbl>

plot(cm, ncol = 3, reorder = TRUE)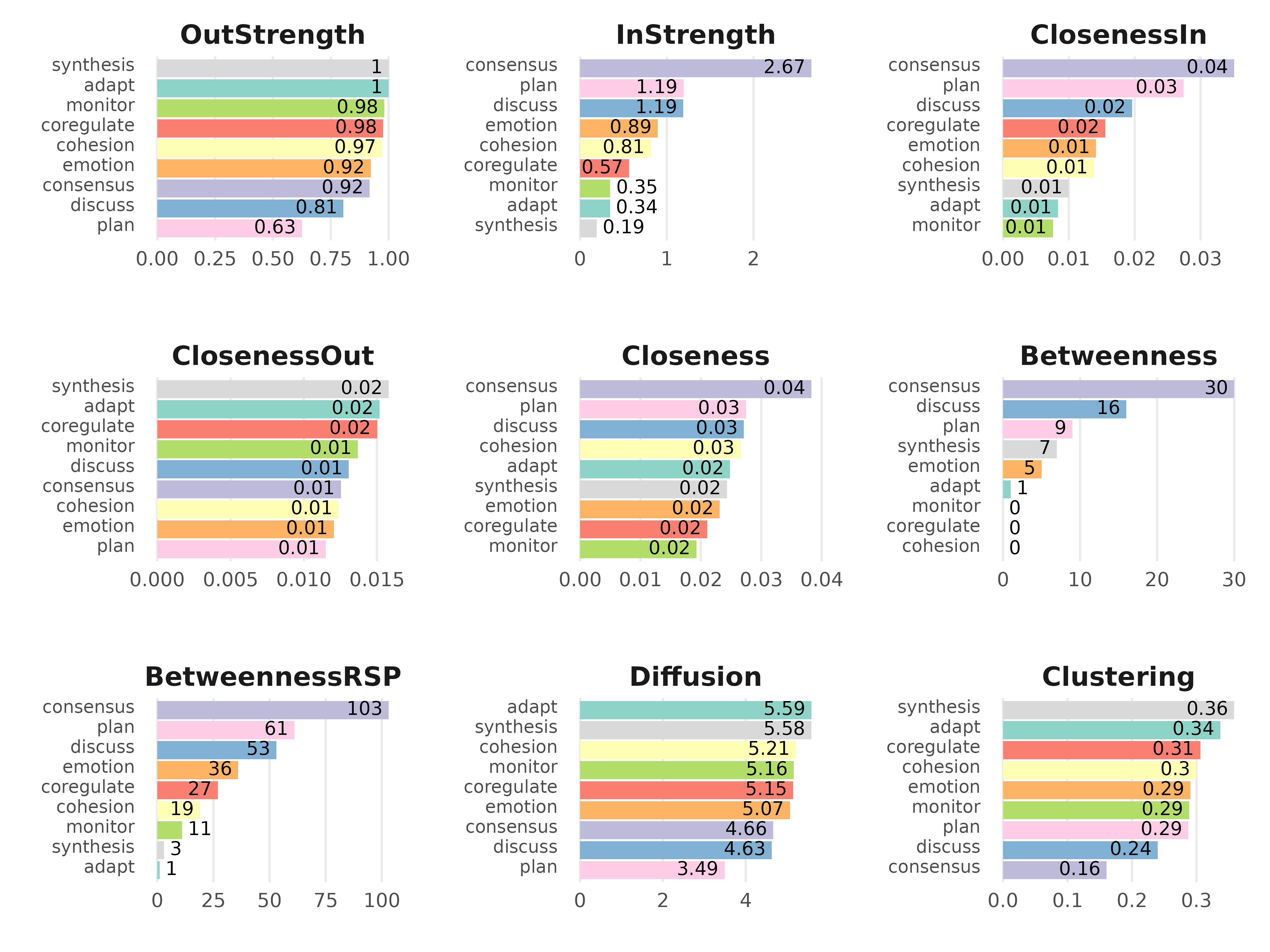

# On group_tna directly
gmodel <- group_model(engagement_mmm)
centralities(gmodel)

#> # A tibble: 9 × 11
#>   group     state      OutStrength InStrength ClosenessIn ClosenessOut Closeness
#> * <chr>     <fct>            <dbl>      <dbl>       <dbl>        <dbl>     <dbl>
#> 1 Cluster 1 Active           0.140      0.360      0.0794       0.0342    0.0794
#> 2 Cluster 1 Average          0.458      0.251      0.0575       0.0994    0.107 
#> 3 Cluster 1 Disengaged       0.210      0.197      0.0401       0.0642    0.0642
#> 4 Cluster 2 Active           0.159      0.248      0.0608       0.0618    0.0787
#> 5 Cluster 2 Average          0.370      0.670      0.121        0.0734    0.121 
#> 6 Cluster 2 Disengaged       0.667      0.278      0.0742       0.119     0.119 
#> 7 Cluster 3 Active           0.417      0.153      0.0678       0.117     0.117 
#> 8 Cluster 3 Average          0.181      0.725      0.148        0.0605    0.148 
#> 9 Cluster 3 Disengaged       0.6        0.319      0.0746       0.101     0.196 
#> # ℹ 4 more variables: Betweenness <dbl>, BetweennessRSP <dbl>, Diffusion <dbl>,
#> #   Clustering <dbl>

`betweenness_network()`

Build network with edge betweenness as weights.

model <- tna(group_regulation)
bn <- betweenness_network(model)
print(bn)

#> State Labels : 
#> 
#>    adapt, cohesion, consensus, coregulate, discuss, emotion, monitor, plan, synthesis 
#> 
#> Edge Betweenness Matrix :
#> 
#>            adapt cohesion consensus coregulate discuss emotion monitor plan
#> adapt          0        0         1          1       0       0       0    3
#> cohesion       0        0         0          6       0       0       2    0
#> consensus      0        0         0          0       0       0       0    4
#> coregulate     8        1         0          0       0       0       0    0
#> discuss        6        0         1          0       0       0       0    0
#> emotion        0        0         0          0       1       0       0    0
#> monitor        0        0         0          0       7       0       0    0
#> plan          11        3         2          3       0       3       3    8
#> synthesis      4        4         3          0       5       6       3    0
#>            synthesis
#> adapt              0
#> cohesion           3
#> consensus          0
#> coregulate         1
#> discuss            1
#> emotion            7
#> monitor           10
#> plan               0
#> synthesis          0
#> 
#> Initial Probabilities : 
#> 
#>      adapt   cohesion  consensus coregulate    discuss    emotion    monitor 
#>     0.0115     0.0605     0.2140     0.0190     0.1755     0.1515     0.1440 
#>       plan  synthesis 
#>     0.2045     0.0195

`estimate_cs()`

Centrality stability via subset sampling.

estimate_cs(x, loops = FALSE, normalize = FALSE,
            measures = c("InStrength", "OutStrength", "Betweenness"),
            iter = 1000, method = "pearson",
            drop_prop = seq(0.1, 0.9, by = 0.1),
            threshold = 0.7, certainty = 0.95, progressbar = FALSE)

model <- tna(group_regulation)
cs <- estimate_cs(model, measures = c("InStrength", "OutStrength"), iter = 100)
print(cs)

#> Centrality Stability Coefficients
#> 
#>  InStrength OutStrength 
#>         0.9         0.9

plot(cs)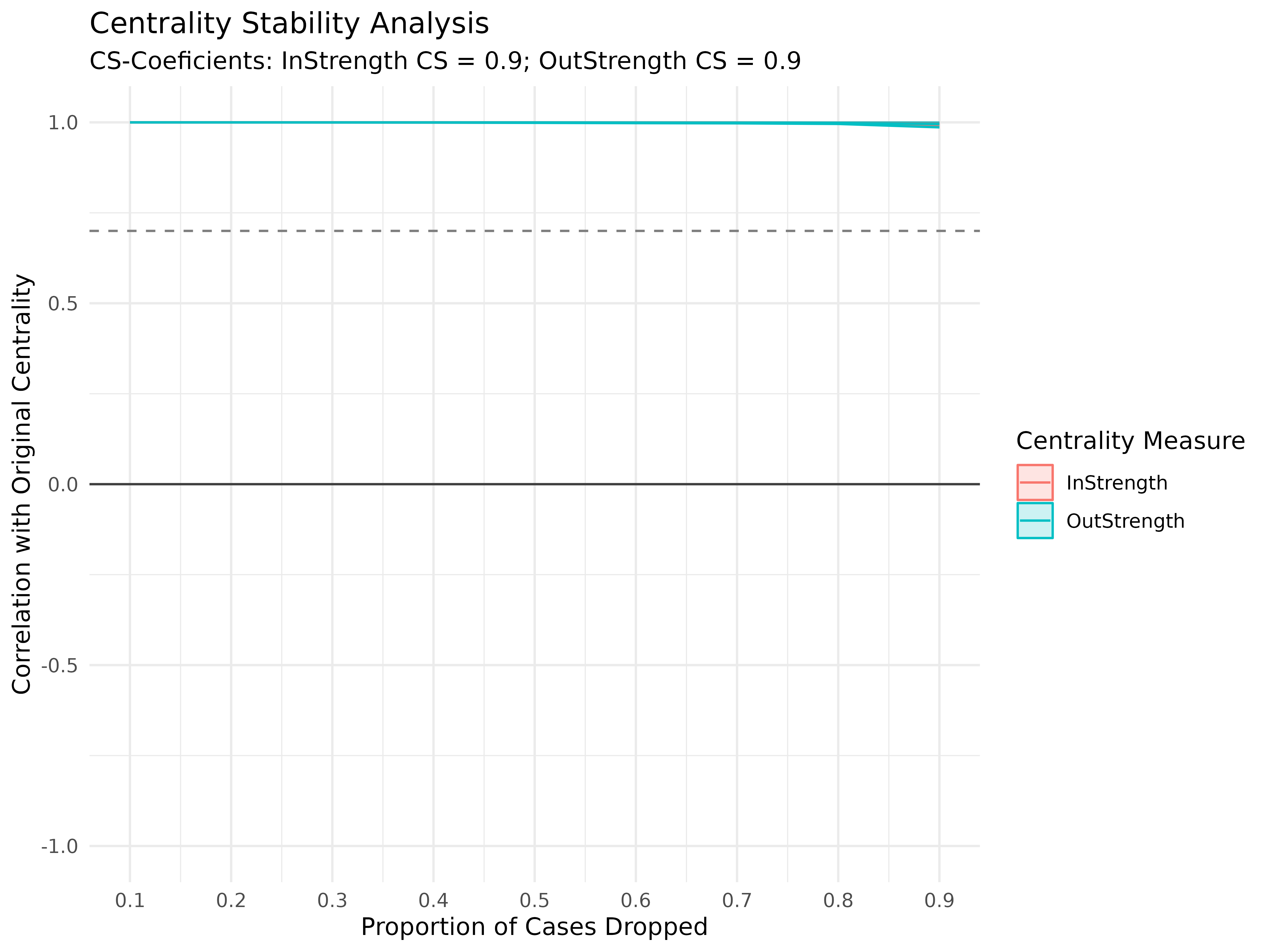

Network Structure

`communities()`

Detect communities using 7 igraph algorithms. Works on tna and group_tna.

communities(x, methods, gamma = 1)

model <- tna(group_regulation)
comm <- communities(model)
print(comm)

#> Number of communities found by each algorithm
#> 
#>         walktrap      fast_greedy       label_prop          infomap 
#>                1                3                1                1 
#> edge_betweenness    leading_eigen        spinglass 
#>                1                3                2 
#> 
#> Community assignments
#> 
#>        state walktrap fast_greedy label_prop infomap edge_betweenness
#> 1      adapt        1           1          1       1                1
#> 2   cohesion        1           1          1       1                1
#> 3  consensus        1           1          1       1                1
#> 4 coregulate        1           2          1       1                1
#> 5    discuss        1           2          1       1                1
#> 6    emotion        1           1          1       1                1
#> 7    monitor        1           2          1       1                1
#> 8       plan        1           3          1       1                1
#> 9  synthesis        1           1          1       1                1
#>   leading_eigen spinglass
#> 1             1         1
#> 2             1         1
#> 3             2         1
#> 4             3         2
#> 5             3         2
#> 6             1         1
#> 7             2         2
#> 8             2         2
#> 9             3         1

plot(comm, method = "spinglass")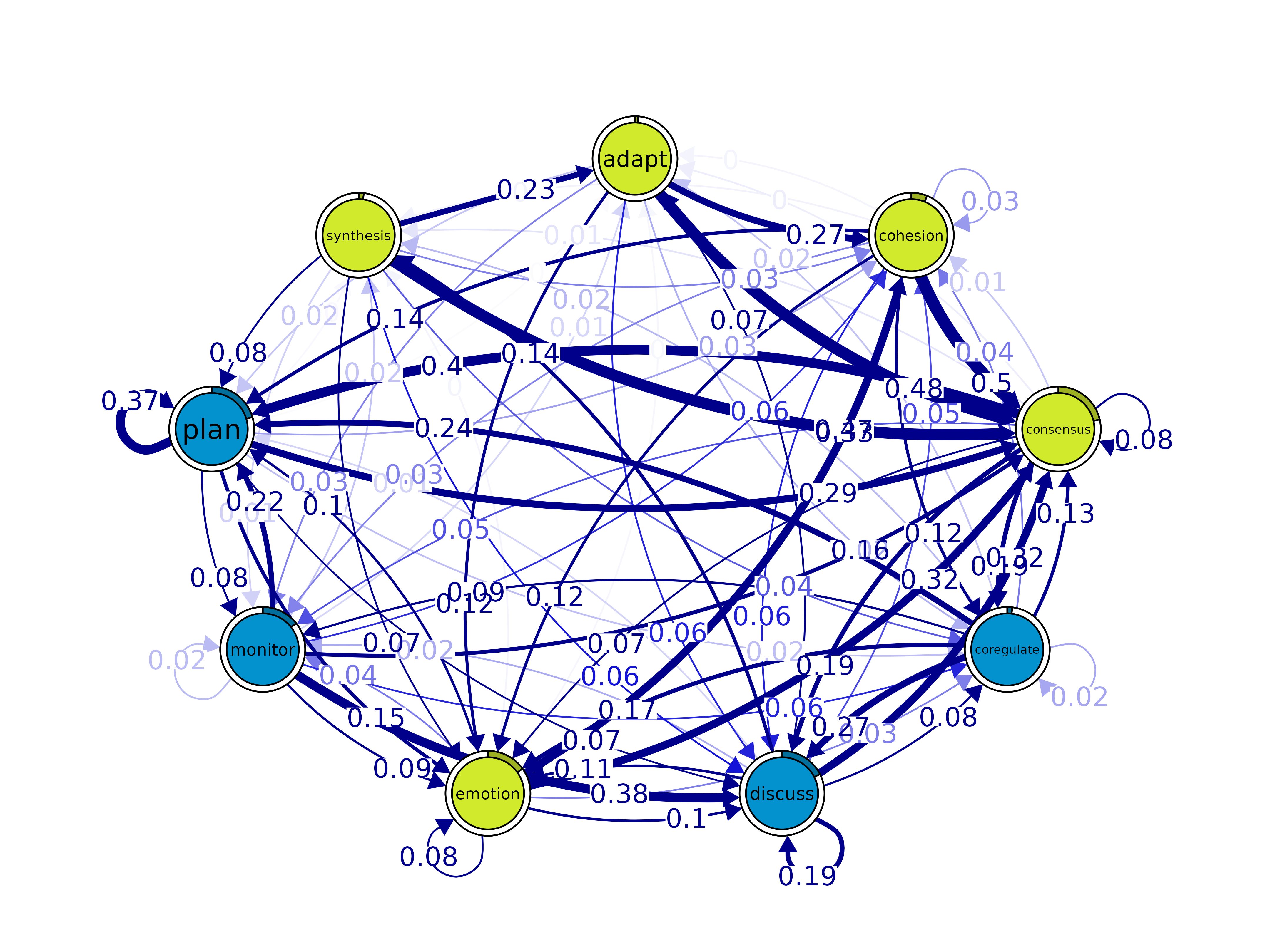

# On group_tna directly
gmodel <- group_model(engagement_mmm)
communities(gmodel)

#> Cluster 1 :
#> Number of communities found by each algorithm
#> 
#>         walktrap      fast_greedy       label_prop          infomap 
#>                1                3                3                1 
#> edge_betweenness    leading_eigen        spinglass 
#>                3                2                1 
#> 
#> Community assignments
#> 
#>        state walktrap fast_greedy label_prop infomap edge_betweenness
#> 1     Active        1           1          1       1                1
#> 2    Average        1           2          2       1                2
#> 3 Disengaged        1           3          3       1                3
#>   leading_eigen spinglass
#> 1             1         1
#> 2             1         1
#> 3             2         1
#> 
#> Cluster 2 :
#> Number of communities found by each algorithm
#> 
#>         walktrap      fast_greedy       label_prop          infomap 
#>                1                2                3                1 
#> edge_betweenness    leading_eigen        spinglass 
#>                2                2                1 
#> 
#> Community assignments
#> 
#>        state walktrap fast_greedy label_prop infomap edge_betweenness
#> 1     Active        1           2          1       1                1
#> 2    Average        1           1          2       1                2
#> 3 Disengaged        1           1          3       1                2
#>   leading_eigen spinglass
#> 1             1         1
#> 2             2         1
#> 3             2         1
#> 
#> Cluster 3 :
#> Number of communities found by each algorithm
#> 
#>         walktrap      fast_greedy       label_prop          infomap 
#>                1                3                3                1 
#> edge_betweenness    leading_eigen        spinglass 
#>                3                2                1 
#> 
#> Community assignments
#> 
#>        state walktrap fast_greedy label_prop infomap edge_betweenness
#> 1     Active        1           1          1       1                1
#> 2    Average        1           2          2       1                2
#> 3 Disengaged        1           3          3       1                3
#>   leading_eigen spinglass
#> 1             1         1
#> 2             2         1
#> 3             2         1

`cliques()`

Identify cliques (complete subgraphs) of a given size.

cliques(x, size = 2, threshold = 0, sum_weights = FALSE, ...)

model <- tna(group_regulation)
cliq <- cliques(model, size = 2)
print(cliq)

#> Number of 2-cliques = 35 (weight threshold = 0)
#> Showing 6 cliques starting from clique number 1
#> 
#> Clique 1
#>            monitor      plan
#> monitor 0.01814375 0.2156315
#> plan    0.07552379 0.3742082
#> 
#> Clique 2
#>            emotion    monitor
#> emotion 0.07684173 0.03630596
#> monitor 0.09071877 0.01814375
#> 
#> Clique 3
#>            emotion       plan
#> emotion 0.07684173 0.09975326
#> plan    0.14682475 0.37420822
#> 
#> Clique 4
#>           discuss    emotion
#> discuss 0.1948874 0.10579600
#> emotion 0.1018682 0.07684173
#> 
#> Clique 5
#>           discuss    monitor
#> discuss 0.1948874 0.02227284
#> monitor 0.3754361 0.01814375
#> 
#> Clique 6
#>            discuss       plan
#> discuss 0.19488737 0.01164262
#> plan    0.06789021 0.37420822

plot(cliq, n = 3, ask = FALSE)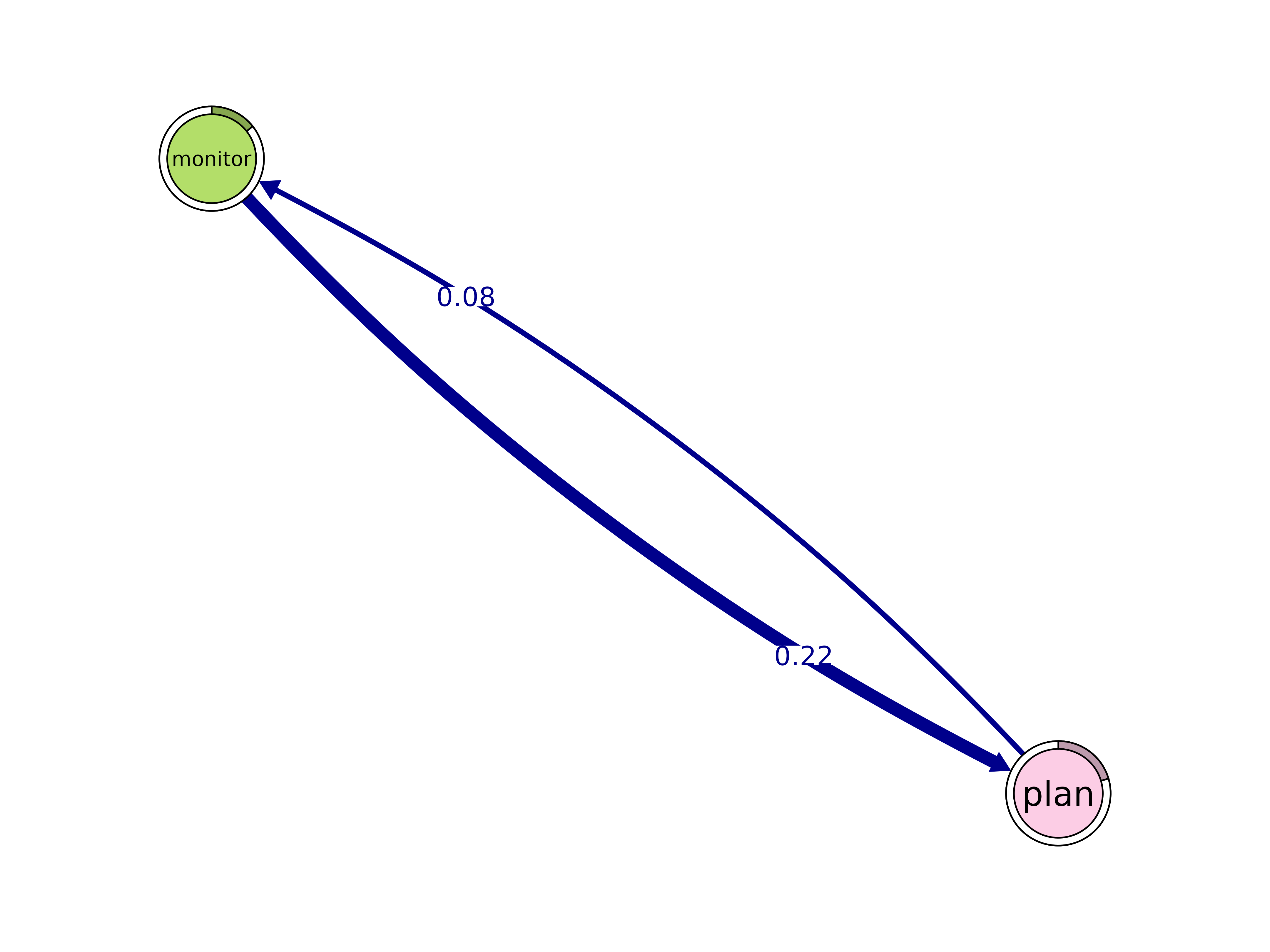

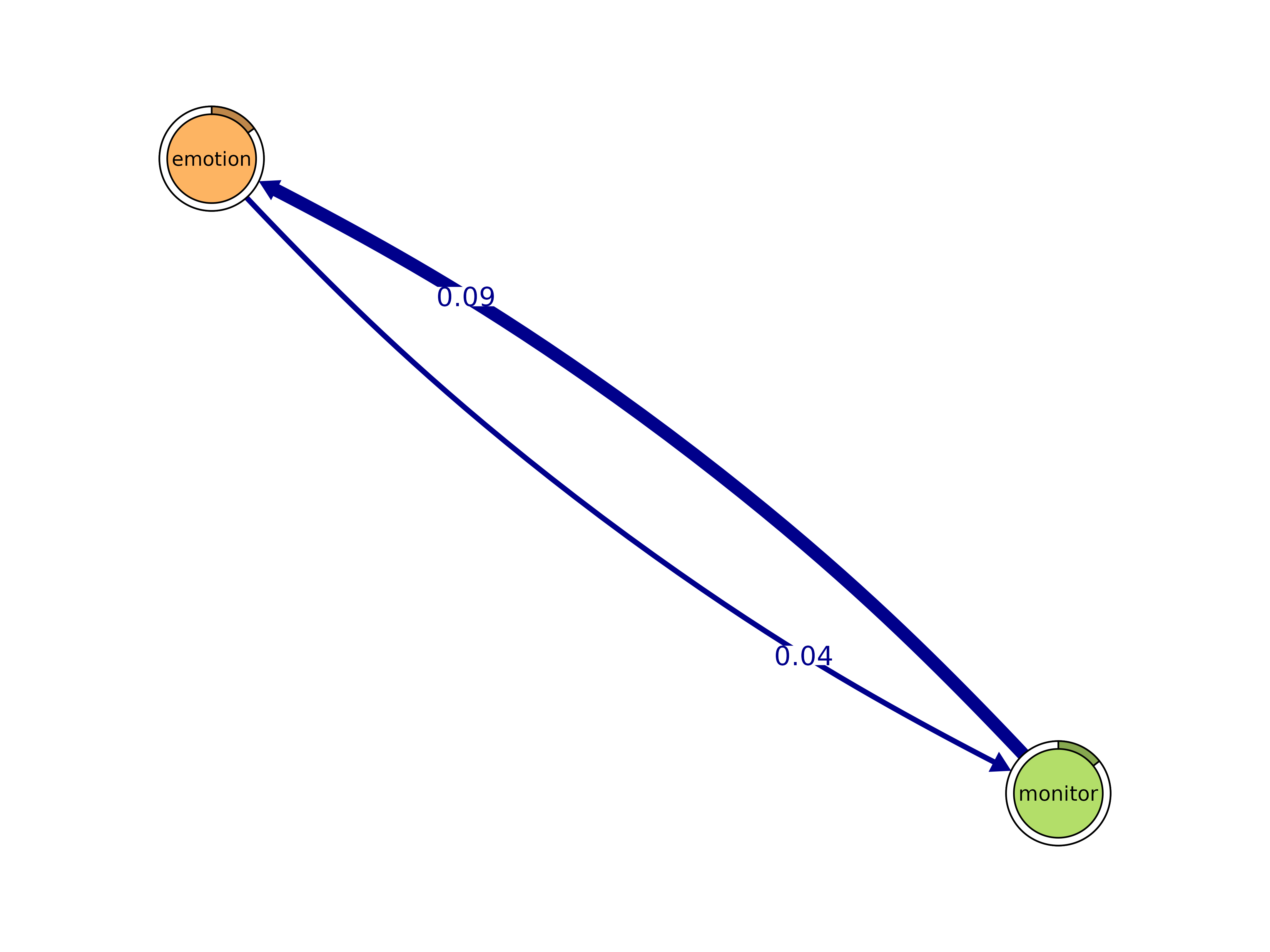
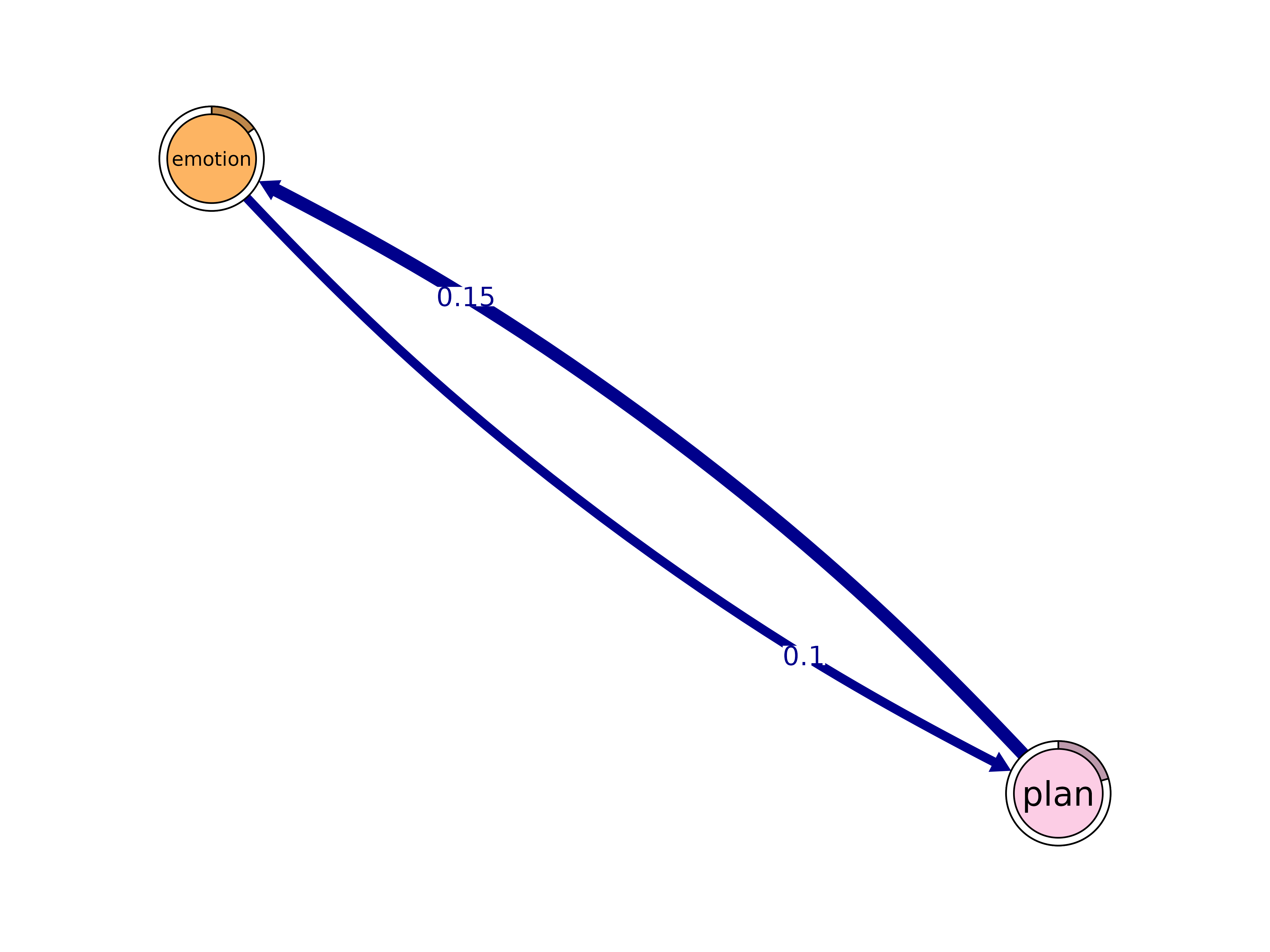
Comparison

`compare()`

Compare two TNA models with comprehensive metrics.

gmodel <- group_model(engagement_mmm)
comp <- compare(gmodel, i = 1, j = 2)
print(comp)

#> Edge difference metrics
#> # A tibble: 9 × 16
#>   source     target     weight_x weight_y raw_difference absolute_difference
#>   <fct>      <fct>         <dbl>    <dbl>          <dbl>               <dbl>
#> 1 Active     Active       0.860    0.841          0.0189              0.0189
#> 2 Average    Active       0.312    0.0926         0.220               0.220 
#> 3 Disengaged Active       0.0479   0.156         -0.108               0.108 
#> 4 Active     Average      0.0892   0.159         -0.0699              0.0699
#> 5 Average    Average      0.542    0.630         -0.0875              0.0875
#> 6 Disengaged Average      0.162    0.511         -0.349               0.349 
#> 7 Active     Disengaged   0.0509   0              0.0509              0.0509
#> 8 Average    Disengaged   0.146    0.278         -0.132               0.132 
#> 9 Disengaged Disengaged   0.790    0.333          0.457               0.457 
#> # ℹ 10 more variables: squared_difference <dbl>, relative_difference <dbl>,
#> #   similarity_strength_index <dbl>, difference_index <dbl>,
#> #   rank_difference <dbl>, percentile_difference <dbl>,
#> #   logarithmic_ratio <dbl>, standardized_weight_x <dbl>,
#> #   standardized_weight_y <dbl>, standardized_score_inflation <dbl>
#> 
#> Summary metrics of differences
#> # A tibble: 22 × 3
#>    category          metric               value
#>    <chr>             <chr>                <dbl>
#>  1 Weight Deviations Mean Abs. Diff.      0.166
#>  2 Weight Deviations Median Abs. Diff.    0.108
#>  3 Weight Deviations RMS Diff.            0.217
#>  4 Weight Deviations Max Abs. Diff.       0.457
#>  5 Weight Deviations Rel. Mean Abs. Diff. 0.498
#>  6 Weight Deviations CV Ratio             1.16 
#>  7 Correlations      Pearson              0.710
#>  8 Correlations      Spearman             0.733
#>  9 Correlations      Kendall              0.611
#> 10 Correlations      Distance             0.500
#> # ℹ 12 more rows
#> 
#> Network metrics
#> # A tibble: 13 × 3
#>    metric                          x     y
#>    <chr>                       <dbl> <dbl>
#>  1 Node Count                  3     3    
#>  2 Edge Count                  9     8    
#>  3 Network Density             1     1    
#>  4 Mean Distance               0.111 0.239
#>  5 Mean Out-Strength           1     1    
#>  6 SD Out-Strength             0.214 0.353
#>  7 Mean In-Strength            1     1    
#>  8 SD In-Strength              0     0    
#>  9 Mean Out-Degree             3     2.67 
#> 10 SD Out-Degree               0     0.577
#> 11 Centralization (Out-Degree) 0     0.25 
#> 12 Centralization (In-Degree)  0     0.25 
#> 13 Reciprocity                 1     0.8

plot(comp)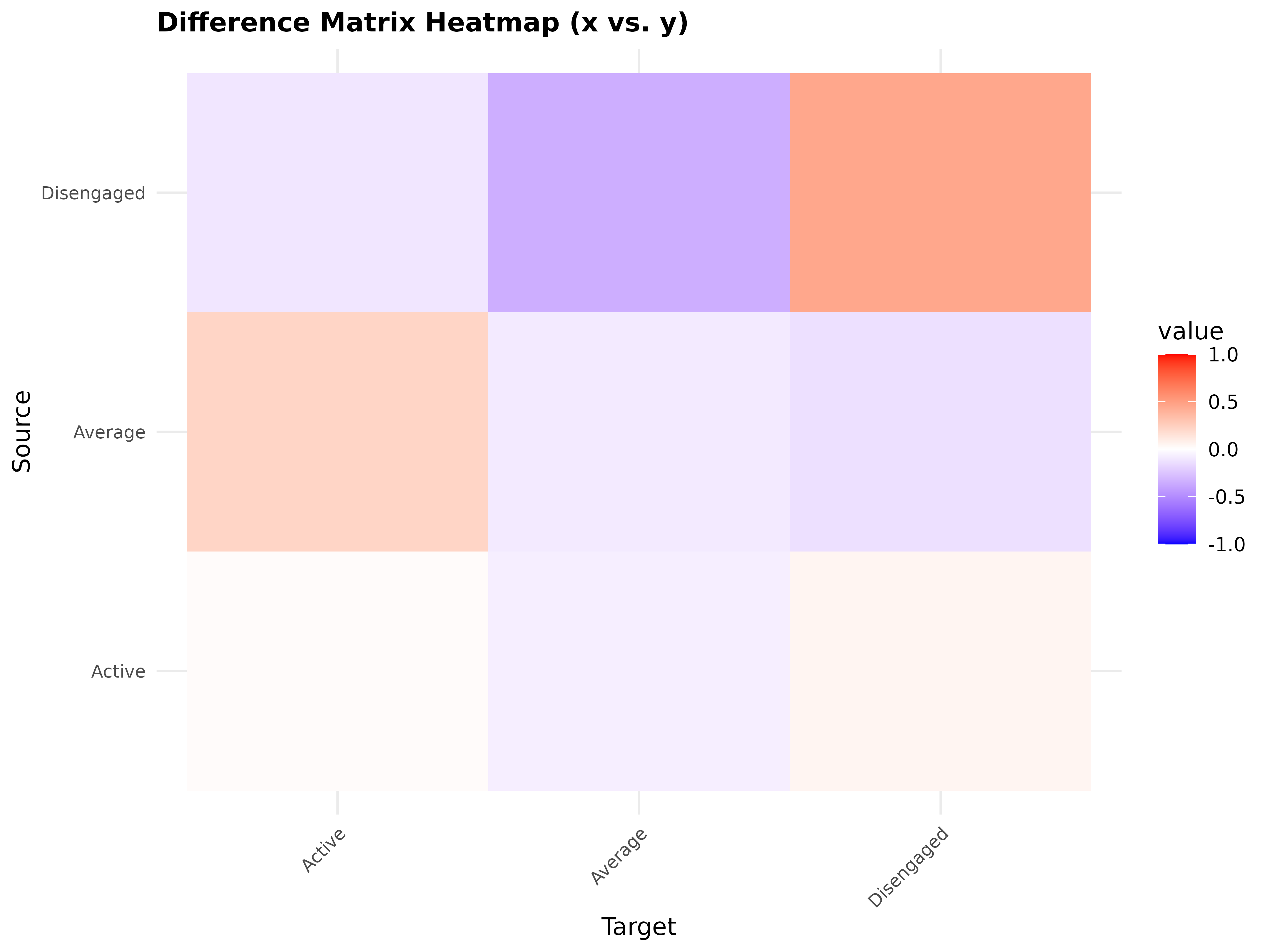

`compare_sequences()`

Compare subsequence patterns between groups. Pass group_tna directly.

# For group_tna (groups already defined)
compare_sequences(x, sub, min_freq = 5L, correction = "bonferroni", ...)

gmodel <- group_model(engagement_mmm)
comp_seq <- compare_sequences(gmodel)
print(head(comp_seq, 10))

#>                                  pattern freq_Cluster 1 freq_Cluster 2
#> 1                                Average           5069            113
#> 2                       Average->Average           2647             68
#> 4                    Disengaged->Average           1057             23
#> 5                 Disengaged->Disengaged           5163             15
#> 7              Average->Average->Average           1350             44
#> 10          Disengaged->Average->Average            565             14
#> 12                            Disengaged           6804             47
#> 15    Average->Average->Average->Average            680             29
#> 20 Disengaged->Average->Average->Average            288              9
#> 22                                Active          12264            137
#>    freq_Cluster 3 prop_Cluster 1 prop_Cluster 2 prop_Cluster 3 effect_size
#> 1              74     0.21000953     0.38047138     0.61157025   10.510487
#> 2              59     0.11432150     0.23859649     0.50862069   11.215353
#> 4              12     0.04565086     0.08070175     0.10344828    5.601244
#> 5               8     0.22298523     0.05263158     0.06896552    4.256135
#> 7              45     0.06089035     0.16117216     0.40540541   12.287328
#> 10             11     0.02548374     0.05128205     0.09909910    6.772509
#> 12             22     0.28189087     0.15824916     0.18181818    2.272492
#> 15             33     0.03209364     0.11111111     0.31132075   12.628119
#> 20              9     0.01359260     0.03448276     0.08490566    8.264617
#> 22             25     0.50809960     0.46127946     0.20661157    1.917857
#>        p_value
#> 1  0.002997003
#> 2  0.008991009
#> 4  0.008991009
#> 5  0.008991009
#> 7  0.026973027
#> 10 0.026973027
#> 12 0.080919081
#> 15 0.080919081
#> 20 0.080919081
#> 22 0.149850150

plot(comp_seq)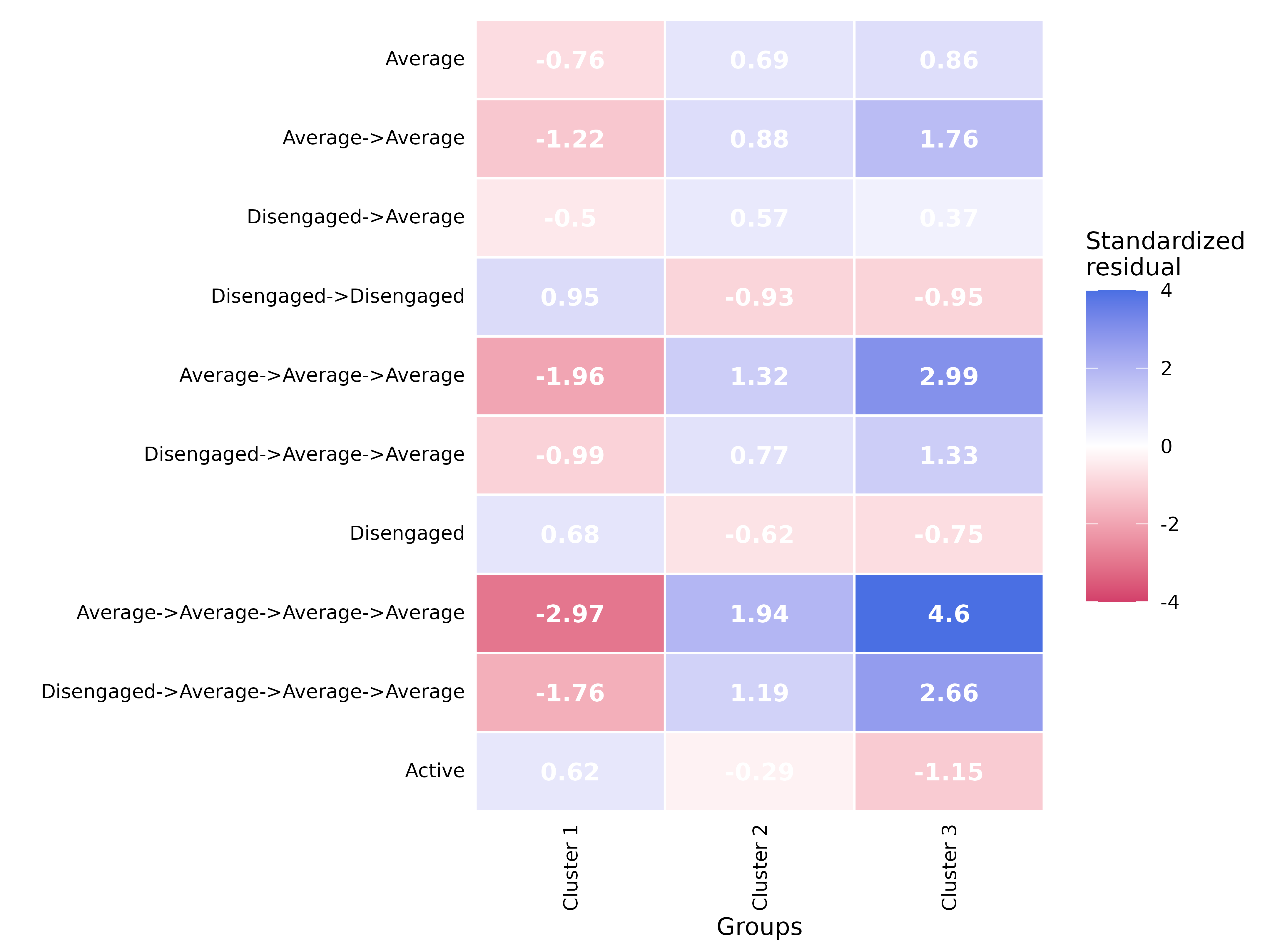

`permutation_test()`

Permutation tests for edge weight and centrality differences.

permutation_test(x, y, adjust = "none", iter = 1000, paired = FALSE,
                 level = 0.05, measures = character(0), ...)

model_x <- tna(group_regulation[1:200, ])
model_y <- tna(group_regulation[1001:1200, ])
perm <- permutation_test(model_x, model_y, iter = 100)
print(perm)

#> # A tibble: 81 × 4
#>    edge_name           diff_true effect_size p_value
#>    <chr>                   <dbl>       <dbl>   <dbl>
#>  1 adapt -> adapt       0            NaN     1      
#>  2 cohesion -> adapt    0.00541        0.973 0.792  
#>  3 consensus -> adapt  -0.000679      -0.160 0.782  
#>  4 coregulate -> adapt  0.00769        0.504 0.644  
#>  5 discuss -> adapt    -0.130         -6.51  0.00990
#>  6 emotion -> adapt     0.0101         1.54  0.277  
#>  7 monitor -> adapt    -0.00480       -0.373 0.990  
#>  8 plan -> adapt        0.00339        1.67  0.00990
#>  9 synthesis -> adapt  -0.159         -1.95  0.0396 
#> 10 adapt -> cohesion   -0.0907        -1.18  0.267  
#> # ℹ 71 more rows

plot(perm)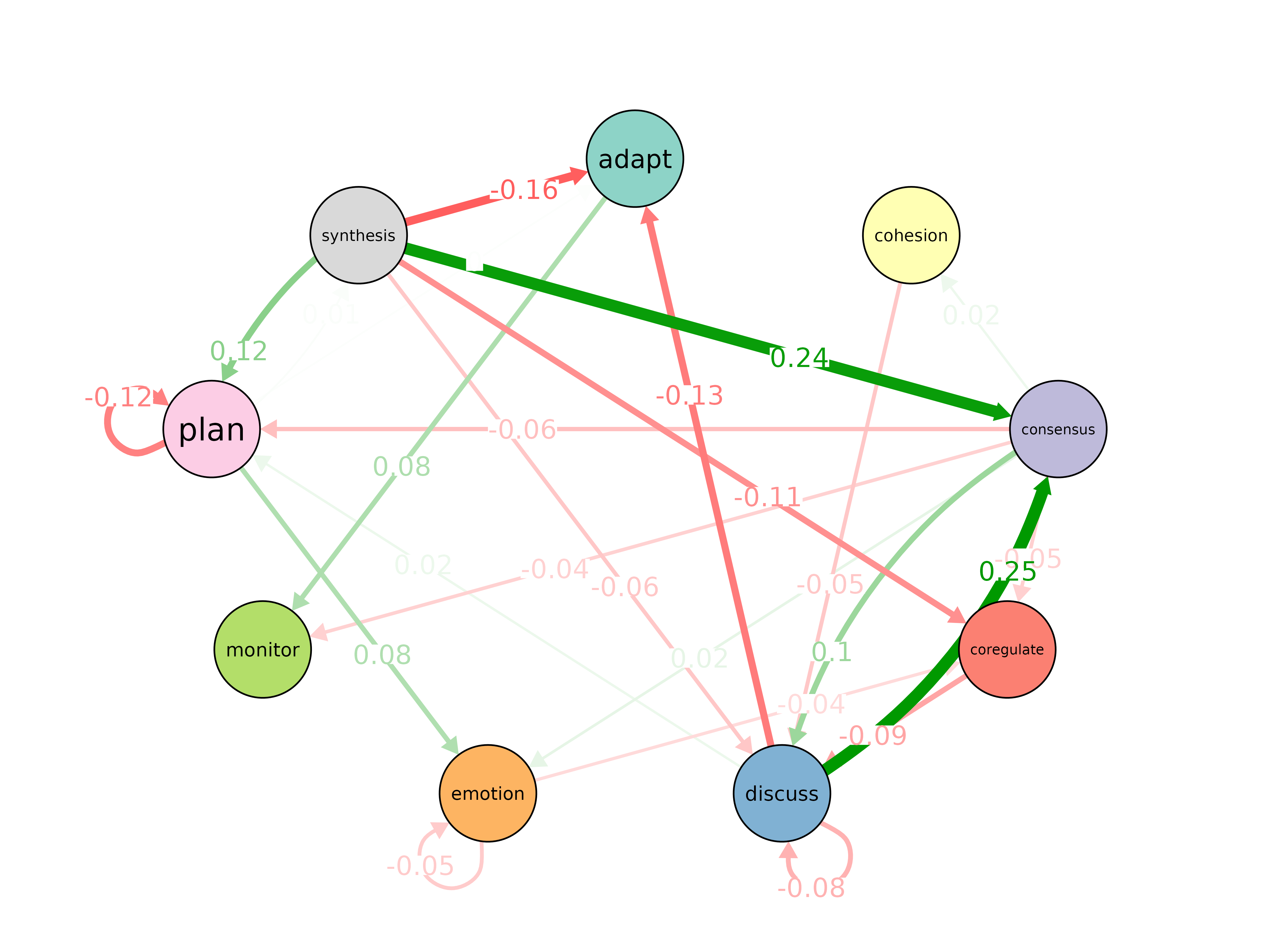

Validation

`bootstrap()`

Bootstrap transition networks for confidence intervals and significance.

bootstrap(x, iter = 1000, level = 0.05, method = "stability",
          threshold, consistency_range = c(0.75, 1.25))

model <- tna(group_regulation)
boot <- bootstrap(model, iter = 100)
print(boot)

#> Significant Edges
#> 
#>          from         to      weight    p_value    cr_lower    cr_upper
#> 5     discuss      adapt 0.071374336 0.00990099 0.053530752 0.089217920
#> 9   synthesis      adapt 0.234662577 0.00990099 0.175996933 0.293328221
#> 10      adapt   cohesion 0.273084479 0.00990099 0.204813360 0.341355599
#> 12  consensus   cohesion 0.014852267 0.02970297 0.011139201 0.018565334
#> 13 coregulate   cohesion 0.036040609 0.02970297 0.027030457 0.045050761
#> 14    discuss   cohesion 0.047582890 0.00990099 0.035687168 0.059478613
#> 15    emotion   cohesion 0.325343673 0.00990099 0.244007755 0.406679591
#> 16    monitor   cohesion 0.055826936 0.01980198 0.041870202 0.069783671
#> 17       plan   cohesion 0.025174598 0.00990099 0.018880949 0.031468248
#> 19      adapt  consensus 0.477406680 0.00990099 0.358055010 0.596758350
#> 20   cohesion  consensus 0.497935103 0.00990099 0.373451327 0.622418879
#> 21  consensus  consensus 0.082003476 0.00990099 0.061502607 0.102504345
#> 22 coregulate  consensus 0.134517766 0.00990099 0.100888325 0.168147208
#> 23    discuss  consensus 0.321184510 0.00990099 0.240888383 0.401480638
#> 24    emotion  consensus 0.320408883 0.00990099 0.240306662 0.400511103
#> 25    monitor  consensus 0.159106769 0.00990099 0.119330077 0.198883461
#> 26       plan  consensus 0.290401169 0.00990099 0.217800877 0.363001462
#> 27  synthesis  consensus 0.466257669 0.00990099 0.349693252 0.582822086
#> 29   cohesion coregulate 0.119174041 0.00990099 0.089380531 0.148967552
#> 30  consensus coregulate 0.187707379 0.00990099 0.140780534 0.234634223
#> 32    discuss coregulate 0.084282460 0.00990099 0.063211845 0.105353075
#> 33    emotion coregulate 0.034191047 0.02970297 0.025643285 0.042738809
#> 34    monitor coregulate 0.057920447 0.04950495 0.043440335 0.072400558
#> 35       plan coregulate 0.017216177 0.02970297 0.012912133 0.021520221
#> 38   cohesion    discuss 0.059587021 0.03960396 0.044690265 0.074483776
#> 39  consensus    discuss 0.188023384 0.00990099 0.141017538 0.235029231
#> 40 coregulate    discuss 0.273604061 0.00990099 0.205203046 0.342005076
#> 41    discuss    discuss 0.194887370 0.00990099 0.146165528 0.243609213
#> 42    emotion    discuss 0.101868171 0.00990099 0.076401128 0.127335213
#> 43    monitor    discuss 0.375436148 0.00990099 0.281577111 0.469295185
#> 44       plan    discuss 0.067890206 0.00990099 0.050917655 0.084862758
#> 46      adapt    emotion 0.119842829 0.02970297 0.089882122 0.149803536
#> 47   cohesion    emotion 0.115634218 0.00990099 0.086725664 0.144542773
#> 48  consensus    emotion 0.072681308 0.00990099 0.054510981 0.090851635
#> 49 coregulate    emotion 0.172081218 0.00990099 0.129060914 0.215101523
#> 50    discuss    emotion 0.105796001 0.00990099 0.079347001 0.132245001
#> 51    emotion    emotion 0.076841734 0.00990099 0.057631301 0.096052168
#> 52    monitor    emotion 0.090718772 0.00990099 0.068039079 0.113398465
#> 53       plan    emotion 0.146824752 0.00990099 0.110118564 0.183530940
#> 56   cohesion    monitor 0.033038348 0.00990099 0.024778761 0.041297935
#> 57  consensus    monitor 0.046610839 0.00990099 0.034958129 0.058263549
#> 58 coregulate    monitor 0.086294416 0.00990099 0.064720812 0.107868020
#> 59    discuss    monitor 0.022272842 0.01980198 0.016704632 0.027841053
#> 60    emotion    monitor 0.036305957 0.02970297 0.027229468 0.045382446
#> 62       plan    monitor 0.075523794 0.00990099 0.056642846 0.094404743
#> 65   cohesion       plan 0.141002950 0.00990099 0.105752212 0.176253687
#> 66  consensus       plan 0.395797124 0.00990099 0.296847843 0.494746405
#> 67 coregulate       plan 0.239086294 0.00990099 0.179314721 0.298857868
#> 69    emotion       plan 0.099753260 0.00990099 0.074814945 0.124691576
#> 70    monitor       plan 0.215631542 0.00990099 0.161723657 0.269539428
#> 71       plan       plan 0.374208218 0.00990099 0.280656164 0.467760273
#> 75  consensus  synthesis 0.007584137 0.03960396 0.005688102 0.009480171
#> 77    discuss  synthesis 0.140976968 0.00990099 0.105732726 0.176221210
#>      ci_lower    ci_upper
#> 5  0.06407889 0.079344928
#> 9  0.20262467 0.264048305
#> 10 0.24380220 0.314926878
#> 12 0.01193752 0.018068638
#> 13 0.02952048 0.044112519
#> 14 0.04280475 0.053696710
#> 15 0.30818151 0.342433084
#> 16 0.04542922 0.064855990
#> 17 0.02135775 0.028599051
#> 19 0.43259186 0.519204837
#> 20 0.47311528 0.526584348
#> 21 0.07543133 0.088993732
#> 22 0.11755793 0.146710534
#> 23 0.30940929 0.334669305
#> 24 0.30239585 0.344578689
#> 25 0.14216494 0.179275984
#> 26 0.27704422 0.299862613
#> 27 0.42656828 0.502648353
#> 29 0.10566010 0.137197312
#> 30 0.17851849 0.197319481
#> 32 0.07678818 0.093205612
#> 33 0.02854022 0.041050446
#> 34 0.04829558 0.073368129
#> 35 0.01375824 0.020252806
#> 38 0.04987027 0.071966294
#> 39 0.17650930 0.197521347
#> 40 0.25792588 0.294943074
#> 41 0.18333907 0.207986047
#> 42 0.09196349 0.115948320
#> 43 0.35770062 0.397109371
#> 44 0.06080519 0.075366257
#> 46 0.09246119 0.147375312
#> 47 0.09993669 0.128714912
#> 48 0.06691024 0.078537406
#> 49 0.15404252 0.187475446
#> 50 0.09607444 0.114939118
#> 51 0.06651007 0.086992191
#> 52 0.07796681 0.106183534
#> 53 0.13876175 0.156942499
#> 56 0.02632770 0.040716148
#> 57 0.04158792 0.052427852
#> 58 0.07501262 0.101438198
#> 59 0.01763099 0.025829327
#> 60 0.02973201 0.044847101
#> 62 0.06829108 0.080602613
#> 65 0.12200665 0.159920483
#> 66 0.38459224 0.408894398
#> 67 0.22235480 0.255320592
#> 69 0.08994246 0.109128945
#> 70 0.19349054 0.235120538
#> 71 0.36318028 0.386516509
#> 75 0.00586061 0.009504858
#> 77 0.13132376 0.153049585
#> 
#> Non-significant Edges
#> 
#>          from         to       weight    p_value     cr_lower    cr_upper
#> 2    cohesion      adapt 0.0029498525 0.48514851 0.0022123894 0.003687316
#> 3   consensus      adapt 0.0047400853 0.13861386 0.0035550640 0.005925107
#> 4  coregulate      adapt 0.0162436548 0.15841584 0.0121827411 0.020304569
#> 6     emotion      adapt 0.0024673951 0.49504950 0.0018505464 0.003084244
#> 7     monitor      adapt 0.0111653873 0.38613861 0.0083740405 0.013956734
#> 8        plan      adapt 0.0009745006 0.52475248 0.0007308754 0.001218126
#> 11   cohesion   cohesion 0.0271386431 0.12871287 0.0203539823 0.033923304
#> 18  synthesis   cohesion 0.0337423313 0.18811881 0.0253067485 0.042177914
#> 28      adapt coregulate 0.0216110020 0.39603960 0.0162082515 0.027013752
#> 31 coregulate coregulate 0.0233502538 0.07920792 0.0175126904 0.029187817
#> 36  synthesis coregulate 0.0444785276 0.21782178 0.0333588957 0.055598160
#> 37      adapt    discuss 0.0589390963 0.14851485 0.0442043222 0.073673870
#> 45  synthesis    discuss 0.0628834356 0.09900990 0.0471625767 0.078604294
#> 54  synthesis    emotion 0.0705521472 0.07920792 0.0529141104 0.088190184
#> 55      adapt    monitor 0.0333988212 0.24752475 0.0250491159 0.041748527
#> 61    monitor    monitor 0.0181437544 0.18811881 0.0136078158 0.022679693
#> 63  synthesis    monitor 0.0122699387 0.46534653 0.0092024540 0.015337423
#> 64      adapt       plan 0.0157170923 0.42574257 0.0117878193 0.019646365
#> 68    discuss       plan 0.0116426221 0.11881188 0.0087319666 0.014553278
#> 72  synthesis       plan 0.0751533742 0.10891089 0.0563650307 0.093941718
#> 74   cohesion  synthesis 0.0035398230 0.51485149 0.0026548673 0.004424779
#> 76 coregulate  synthesis 0.0187817259 0.12871287 0.0140862944 0.023477157
#> 78    emotion  synthesis 0.0028198802 0.41584158 0.0021149101 0.003524850
#> 79    monitor  synthesis 0.0160502442 0.26732673 0.0120376832 0.020062805
#> 80       plan  synthesis 0.0017865844 0.41584158 0.0013399383 0.002233230
#>        ci_lower    ci_upper
#> 2  0.0005753743 0.005349977
#> 3  0.0034687585 0.006278361
#> 4  0.0098108520 0.020646139
#> 6  0.0010528071 0.004212903
#> 7  0.0057816442 0.015234127
#> 8  0.0001632893 0.001757592
#> 11 0.0202648251 0.035016631
#> 18 0.0229575499 0.046770918
#> 28 0.0079738048 0.034568888
#> 31 0.0174920382 0.030689101
#> 36 0.0255617245 0.062541457
#> 37 0.0420007471 0.077659237
#> 45 0.0431674805 0.082822958
#> 54 0.0532226587 0.093211422
#> 55 0.0198099674 0.050070748
#> 61 0.0100512338 0.024489377
#> 63 0.0063206033 0.020124590
#> 64 0.0069561163 0.028798166
#> 68 0.0083982748 0.014872118
#> 72 0.0584608476 0.099699375
#> 74 0.0005983651 0.005961536
#> 76 0.0135304505 0.025452780
#> 78 0.0010456607 0.004767214
#> 79 0.0096810848 0.024359445
#> 80 0.0009564382 0.003008823

plot(boot)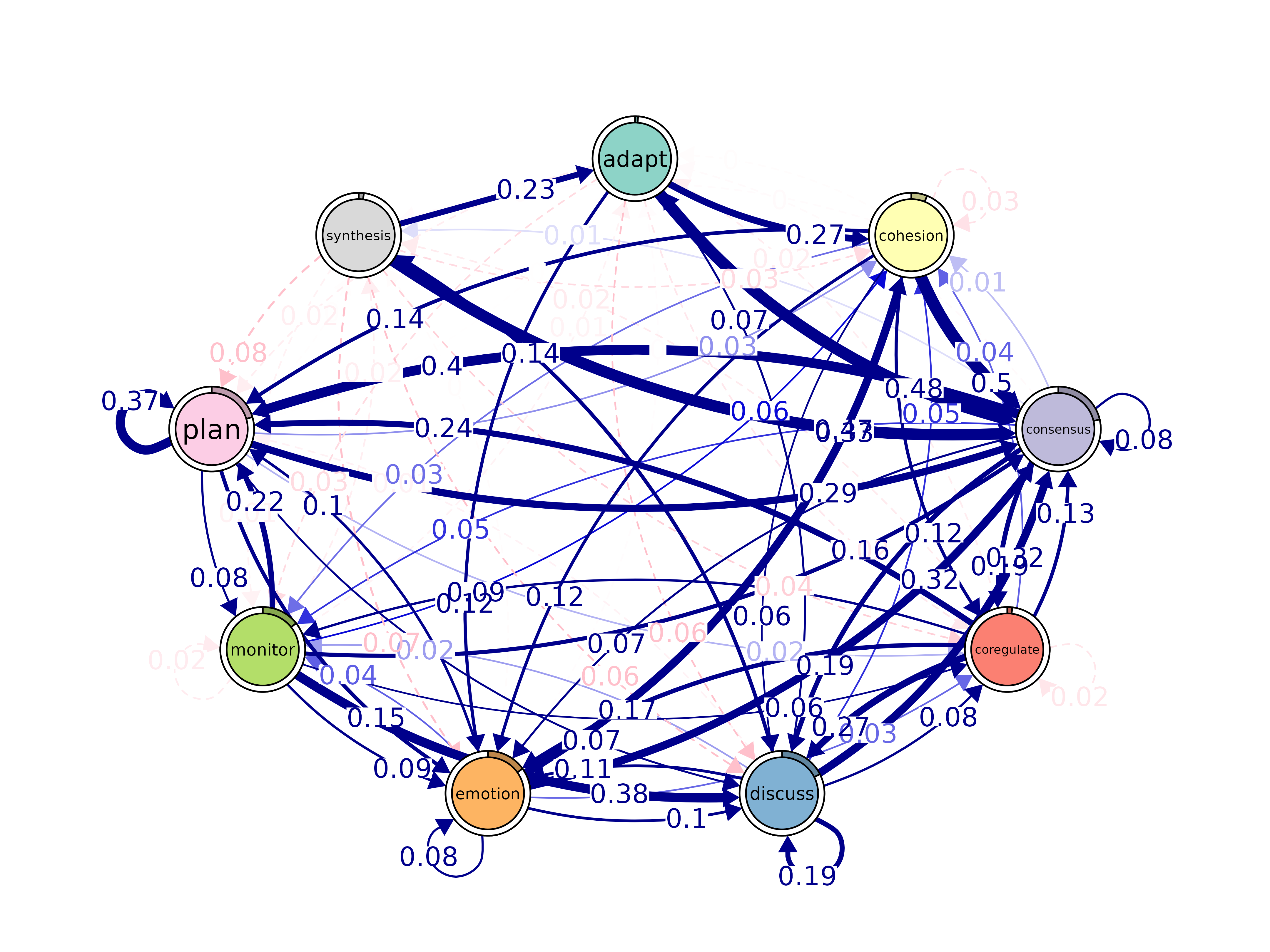

`bootstrap_cliques()`

Bootstrap cliques to assess stability.

bc <- bootstrap_cliques(model, size = 2, iter = 100)
print(bc)

#>                  clique mean_weight   p_values   sig    cr_lower   cr_upper
#> 1        plan-synthesis  0.11278704 0.35643564 FALSE 0.084590283 0.14098381
#> 2          monitor-plan  0.17087683 0.19801980 FALSE 0.128157620 0.21359603
#> 3     monitor-synthesis  0.01161598 0.79207921 FALSE 0.008711988 0.01451998
#> 4       emotion-monitor  0.05550255 0.50495050 FALSE 0.041626916 0.06937819
#> 5          emotion-plan  0.17440699 0.00990099  TRUE 0.130805243 0.21800874
#> 6     emotion-synthesis  0.03755344 0.68316832 FALSE 0.028165080 0.04694180
#> 7       discuss-emotion  0.11984832 0.82178218 FALSE 0.089886239 0.14981040
#> 8       discuss-monitor  0.15268503 0.94059406 FALSE 0.114513772 0.19085629
#> 9          discuss-plan  0.16215710 0.46534653 FALSE 0.121617828 0.20269638
#> 10    discuss-synthesis  0.09968694 0.22772277 FALSE 0.074765208 0.12460868
#> 11   coregulate-discuss  0.14403104 0.94059406 FALSE 0.108023277 0.18003880
#> 12   coregulate-emotion  0.07661606 0.45544554 FALSE 0.057462047 0.09577008
#> 13   coregulate-monitor  0.04642722 0.41584158 FALSE 0.034820413 0.05803402
#> 14      coregulate-plan  0.16346524 0.42574257 FALSE 0.122598927 0.20433154
#> 15 coregulate-synthesis  0.02165263 0.89108911 FALSE 0.016239470 0.02706578
#> 16 consensus-coregulate  0.10689472 0.25742574 FALSE 0.080171039 0.13361840
#> 17    consensus-discuss  0.19652469 0.01980198  TRUE 0.147393514 0.24565586
#> 18    consensus-emotion  0.13798385 0.11881188 FALSE 0.103487888 0.17247981
#> 19    consensus-monitor  0.07646621 0.87128713 FALSE 0.057349657 0.09558276
#> 20       consensus-plan  0.28560250 0.00990099  TRUE 0.214201873 0.35700312
#> 21  consensus-synthesis  0.13896132 0.46534653 FALSE 0.104220990 0.17370165
#> 22   cohesion-consensus  0.15548237 0.38613861 FALSE 0.116611779 0.19435297
#> 23  cohesion-coregulate  0.05142589 0.70297030 FALSE 0.038569415 0.06428236
#> 24     cohesion-discuss  0.08229898 0.39603960 FALSE 0.061724236 0.10287373
#> 25     cohesion-emotion  0.13623957 0.14851485 FALSE 0.102179675 0.17029946
#> 26     cohesion-monitor  0.03353692 0.68316832 FALSE 0.025152690 0.04192115
#> 27        cohesion-plan  0.14188110 0.13861386 FALSE 0.106410827 0.17735138
#> 28   cohesion-synthesis  0.01610520 0.58415842 FALSE 0.012078900 0.02013150
#> 29       adapt-cohesion  0.07579324 0.68316832 FALSE 0.056844933 0.09474155
#> 30      adapt-consensus  0.14103756 0.60396040 FALSE 0.105778170 0.17629695
#> 31     adapt-coregulate  0.01530123 0.86138614 FALSE 0.011475921 0.01912653
#> 32        adapt-discuss  0.08130020 0.99009901 FALSE 0.060975150 0.10162525
#> 33        adapt-emotion  0.04978799 0.88118812 FALSE 0.037340992 0.06223499
#> 34        adapt-monitor  0.01567699 0.75247525 FALSE 0.011757743 0.01959624
#> 35           adapt-plan  0.09772495 0.27722772 FALSE 0.073293715 0.12215619
#> 36      adapt-synthesis  0.05866564 0.69306931 FALSE 0.043999233 0.07333206
#>       ci_lower   ci_upper
#> 1  0.067871551 0.16916223
#> 2  0.145865463 0.24209823
#> 3  0.000000000 0.04886905
#> 4  0.029849425 0.12163425
#> 5  0.142235770 0.21299081
#> 6  0.000000000 0.07106378
#> 7  0.036705096 0.10441189
#> 8  0.046129261 0.11903859
#> 9  0.094095861 0.15261396
#> 10 0.059482265 0.11527209
#> 11 0.041666667 0.11866003
#> 12 0.044193962 0.14108333
#> 13 0.015142463 0.07089650
#> 14 0.088771205 0.16251061
#> 15 0.000000000 0.02670455
#> 16 0.052969881 0.12558519
#> 17 0.185334478 0.24076827
#> 18 0.095754941 0.16349364
#> 19 0.076490398 0.19025012
#> 20 0.235414139 0.30275329
#> 21 0.104114078 0.23946276
#> 22 0.149104647 0.23333459
#> 23 0.040210704 0.12331597
#> 24 0.038884437 0.11526961
#> 25 0.092156880 0.14994310
#> 26 0.023060423 0.08172764
#> 27 0.082919711 0.15436799
#> 28 0.000000000 0.03506944
#> 29 0.012500000 0.24109375
#> 30 0.015196159 0.18507025
#> 31 0.000000000 0.03125000
#> 32 0.011104249 0.05388393
#> 33 0.004423167 0.18288826
#> 34 0.000000000 0.04886905
#> 35 0.060602139 0.10098269
#> 36 0.000000000 0.09366259

`prune()`

Remove weak edges. Four methods available.

prune(x, method = "threshold", threshold = 0.1, lowest = 0.05,
      level = 0.5, boot = NULL, ...)

model <- tna(group_regulation)

pruned_t <- prune(model, method = "threshold", threshold = 0.1)
pruned_p <- prune(model, method = "lowest", lowest = 0.05)
pruned_d <- prune(model, method = "disparity", level = 0.5)

pruning_details(pruned_t)

#> **Pruning Details**
#> 
#> Method used: User-specified threshold (0.1)
#> Number of removed edges: 49
#> Number of retained edges: 29
#> 
#> **Removed edges**
#> 
#>          from         to       weight
#> 1    cohesion      adapt 0.0029498525
#> 2   consensus      adapt 0.0047400853
#> 3  coregulate      adapt 0.0162436548
#> 4     discuss      adapt 0.0713743356
#> 5     emotion      adapt 0.0024673951
#> 6     monitor      adapt 0.0111653873
#> 7        plan      adapt 0.0009745006
#> 8    cohesion   cohesion 0.0271386431
#> 9   consensus   cohesion 0.0148522673
#> 10 coregulate   cohesion 0.0360406091
#> 11    discuss   cohesion 0.0475828904
#> 12    monitor   cohesion 0.0558269365
#> 13       plan   cohesion 0.0251745980
#> 14  synthesis   cohesion 0.0337423313
#> 15  consensus  consensus 0.0820034761
#> 16      adapt coregulate 0.0216110020
#> 17 coregulate coregulate 0.0233502538
#> 18    discuss coregulate 0.0842824601
#> 19    emotion coregulate 0.0341910469
#> 20    monitor coregulate 0.0579204466
#> 21       plan coregulate 0.0172161767
#> 22  synthesis coregulate 0.0444785276
#> 23      adapt    discuss 0.0589390963
#> 24   cohesion    discuss 0.0595870206
#> 25       plan    discuss 0.0678902063
#> 26  synthesis    discuss 0.0628834356
#> 27  consensus    emotion 0.0726813083
#> 28    emotion    emotion 0.0768417342
#> 29    monitor    emotion 0.0907187718
#> 30  synthesis    emotion 0.0705521472
#> 31      adapt    monitor 0.0333988212
#> 32   cohesion    monitor 0.0330383481
#> 33  consensus    monitor 0.0466108390
#> 34 coregulate    monitor 0.0862944162
#> 35    discuss    monitor 0.0222728423
#> 36    emotion    monitor 0.0363059570
#> 37    monitor    monitor 0.0181437544
#> 38       plan    monitor 0.0755237941
#> 39  synthesis    monitor 0.0122699387
#> 40      adapt       plan 0.0157170923
#> 41    discuss       plan 0.0116426221
#> 42    emotion       plan 0.0997532605
#> 43  synthesis       plan 0.0751533742
#> 44   cohesion  synthesis 0.0035398230
#> 45  consensus  synthesis 0.0075841365
#> 46 coregulate  synthesis 0.0187817259
#> 47    emotion  synthesis 0.0028198802
#> 48    monitor  synthesis 0.0160502442
#> 49       plan  synthesis 0.0017865844

plot(pruned_t)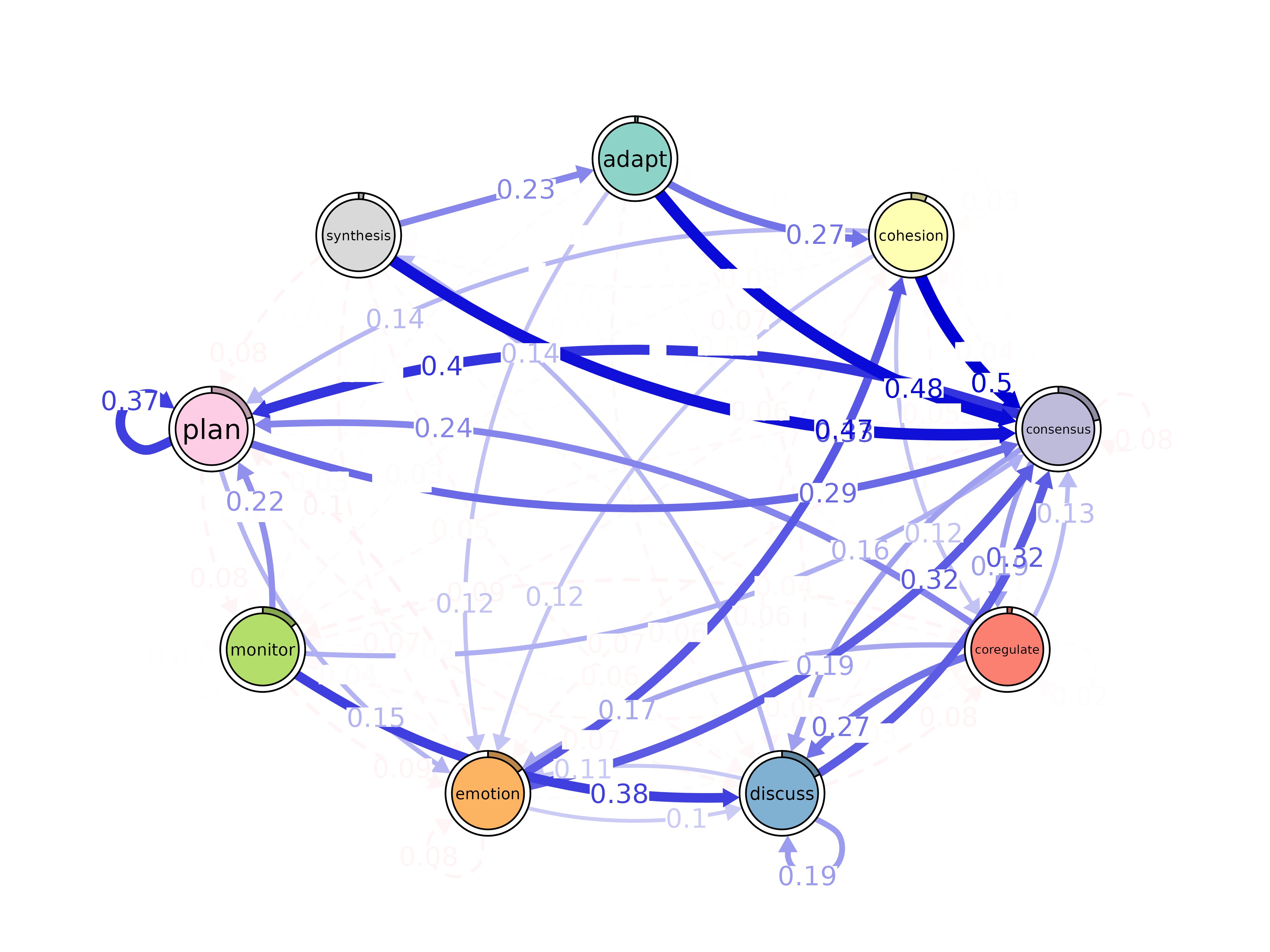

# Restore and reapply
restored <- deprune(pruned_t)
repruned <- reprune(restored)

Clustering

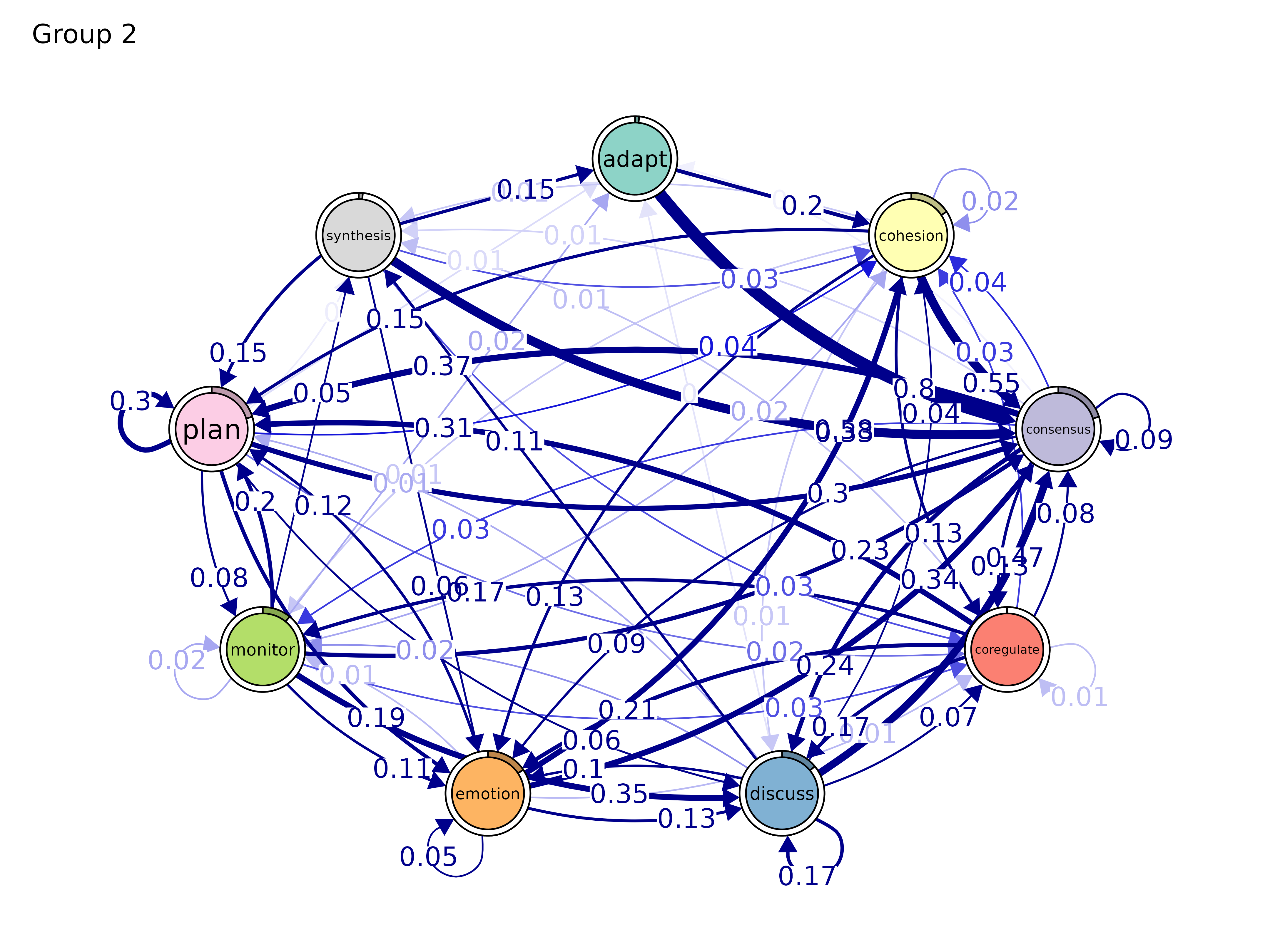
`cluster_sequences()`

Cluster sequences using string distance-based dissimilarity.

cluster_sequences(data, k, dissimilarity = "hamming", method = "pam",
                  na_syms = c("*", "%"), weighted = FALSE, lambda = 1, ...)

result <- cluster_sequences(group_regulation[1:200, ], k = 3, dissimilarity = "osa")
print(result)

#> Clustering method: pam 
#> Number of clusters: 3 
#> Silhouette score: 0.520094 
#> Cluster sizes:
#>  1  2  3 
#> 72 64 64

# Pass directly to group_model
gmodel_clust <- group_model(result)
plot(gmodel_clust)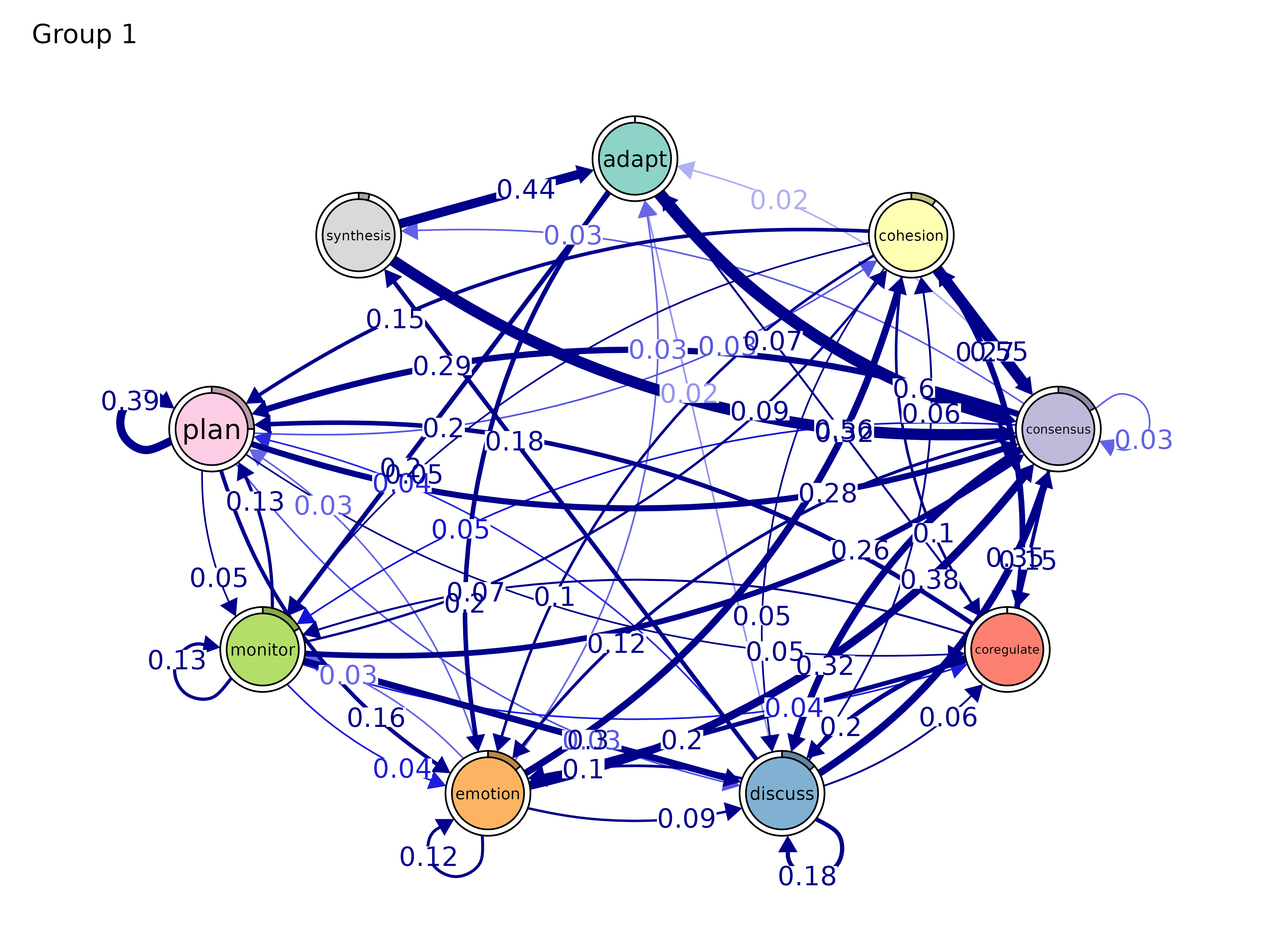

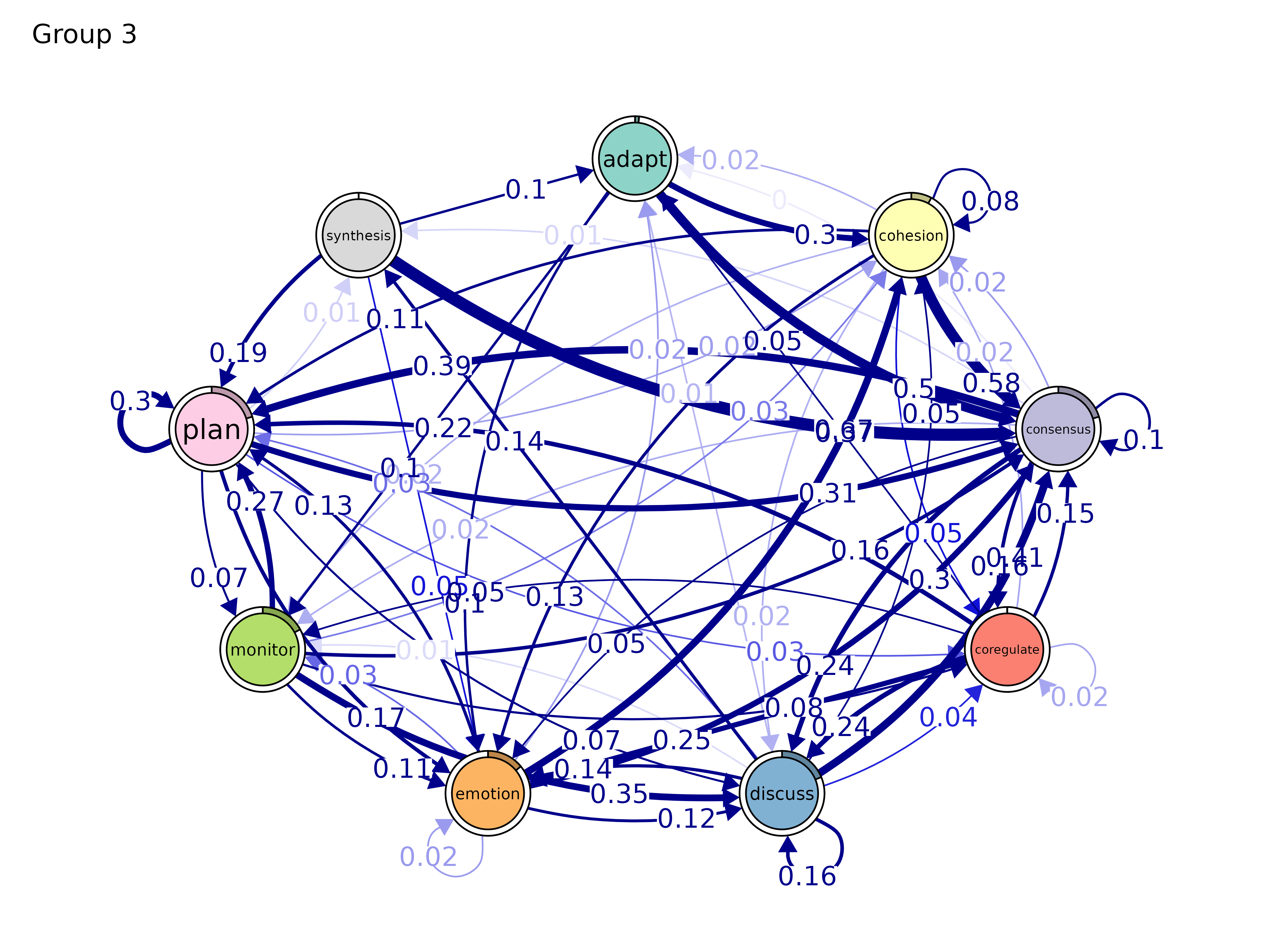
`rename_groups()`

gmodel <- group_model(engagement_mmm)
gmodel_renamed <- rename_groups(gmodel, c("A", "B", "C"))
cat("Original:", names(group_model(engagement_mmm)), "\n")

#> Original: Cluster 1 Cluster 2 Cluster 3

cat("Renamed:", names(gmodel_renamed), "\n")

#> Renamed: A B C

`mmm_stats()`

mmm_stats(engagement_mmm)

#>     cluster    variable  estimate std_error  ci_lower  ci_upper   z_value
#> 1 Cluster 2 (Intercept) -2.640329 0.1274911 -2.890207 -2.390451 -20.70991
#> 2 Cluster 3 (Intercept) -4.512131 0.3157501 -5.130990 -3.893272 -14.29020
#>   p_value
#> 1       0
#> 2       0

Summary & Conversion

`summary()`

model <- tna(group_regulation)
summary(model)

#> # A tibble: 13 × 2
#>    metric                         value
#>  * <chr>                          <dbl>
#>  1 Node Count                  9   e+ 0
#>  2 Edge Count                  7.8 e+ 1
#>  3 Network Density             1   e+ 0
#>  4 Mean Distance               4.72e- 2
#>  5 Mean Out-Strength           1   e+ 0
#>  6 SD Out-Strength             8.07e- 1
#>  7 Mean In-Strength            1   e+ 0
#>  8 SD In-Strength              6.80e-17
#>  9 Mean Out-Degree             8.67e+ 0
#> 10 SD Out-Degree               7.07e- 1
#> 11 Centralization (Out-Degree) 1.56e- 2
#> 12 Centralization (In-Degree)  1.56e- 2
#> 13 Reciprocity                 9.86e- 1

gmodel <- group_model(engagement_mmm)
summary(gmodel)

#> # A tibble: 13 × 4
#>    metric                      `Cluster 1` `Cluster 2` `Cluster 3`
#>  * <chr>                             <dbl>       <dbl>       <dbl>
#>  1 Node Count                        3           3           3    
#>  2 Edge Count                        9           8           8    
#>  3 Network Density                   1           1           1    
#>  4 Mean Distance                     0.111       0.239       0.302
#>  5 Mean Out-Strength                 1           1           1    
#>  6 SD Out-Strength                   0.214       0.353       0.472
#>  7 Mean In-Strength                  1           1           1    
#>  8 SD In-Strength                    0           0           0    
#>  9 Mean Out-Degree                   3           2.67        2.67 
#> 10 SD Out-Degree                     0           0.577       0.577
#> 11 Centralization (Out-Degree)       0           0.25        0.25 
#> 12 Centralization (In-Degree)        0           0.25        0.25 
#> 13 Reciprocity                       1           0.8         0.8

`as.igraph()`

model <- tna(group_regulation)
g <- as.igraph(model)
print(g)

#> IGRAPH 0d3f7f5 DNW- 9 78 -- 
#> + attr: name (v/c), weight (e/n)
#> + edges from 0d3f7f5 (vertex names):
#>  [1] adapt     ->cohesion   adapt     ->consensus  adapt     ->coregulate
#>  [4] adapt     ->discuss    adapt     ->emotion    adapt     ->monitor   
#>  [7] adapt     ->plan       cohesion  ->adapt      cohesion  ->cohesion  
#> [10] cohesion  ->consensus  cohesion  ->coregulate cohesion  ->discuss   
#> [13] cohesion  ->emotion    cohesion  ->monitor    cohesion  ->plan      
#> [16] cohesion  ->synthesis  consensus ->adapt      consensus ->cohesion  
#> [19] consensus ->consensus  consensus ->coregulate consensus ->discuss   
#> [22] consensus ->emotion    consensus ->monitor    consensus ->plan      
#> + ... omitted several edges

tna v1.1.0 | MIT License | Mohammed Saqr, Santtu Tikka, Sonsoles Lopez-Pernas

Reference: Saqr M., Lopez-Pernas S., et al. (2025). Transition Network Analysis. Proc. LAK ’25, 351-361. doi:10.1145/3706468.3706513

tna — R Package Documentation

v1.1.0 — Transition Network Analysis

Building Models

build_model()

Model types

group_model() / group_tna()

sna()

Plotting

plot()

plot_frequencies()

plot_mosaic()

plot_sequences()

plot_compare()

plot_associations()

hist()

Additional plot methods

Data Preparation

prepare_data()

import_data()

import_onehot()

simulate()

Centrality Measures

centralities()

betweenness_network()

estimate_cs()